Example 5.2 considered a set of kinked paths about a straight-line path.

(a) Using the same set of alternative paths, suppose one considered the sum of phasors about the path with \(n=50\) instead of the sum about the \(n=0\) straight-line path. In particular, if one summed from \(n=25\) to \(n=75, \pm 25\) about \(n=50\), how would the sum of phasors differ from the sum for paths about \(n=0\) ? What physical conclusion can you draw from this?

(b) Now returning to the set of kinked paths about the straight-line \(n=0\) path, draw the phasor diagram if the wave number \(k\) of the particle were doubled (i.e., if the de Broglie wavelength \(\lambda\) were halved.) What can be concluded about the physical difference between this case and that used in Example 5.2?

Data from Example 5.2

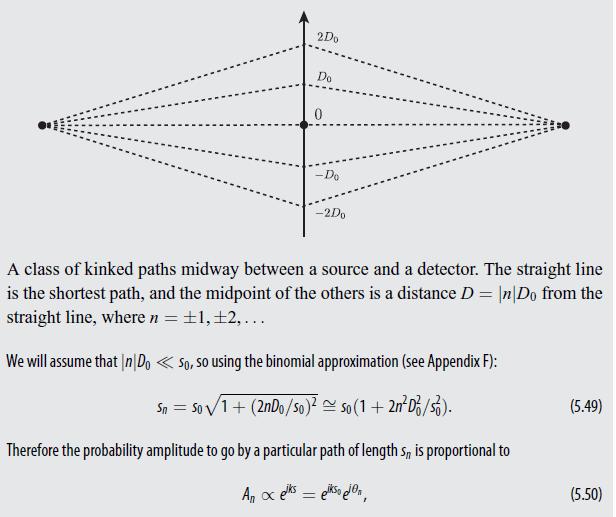
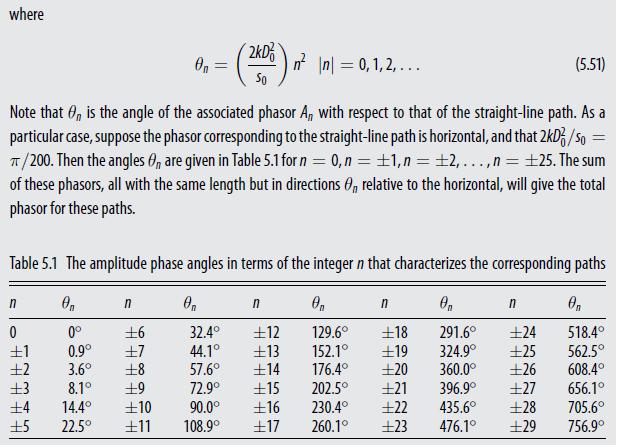
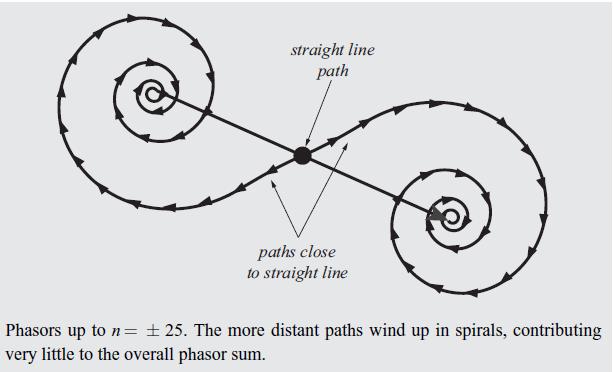
Let so, be the shortest distance between the source and the detector, corresponding to a straight-line path. We will sum the probability amplitudes for a certain subset of all paths near this path. These particular alternate paths consist of a straight line with a kink in the middle, where the kink is a distance D = |n|Do (n= 1,2,...) from the straight line, as shown in Figure 5.18. If the paths have lengths,, then by the Pythagorean theorem (Sn/2)=(so/2)2 + (nDo). (5.48)