A motor under load generates heat internally at a constant rate H and radiates heat, in accordance with Newton’s law of cooling, at a rate kθ, where k is a constant and θ is the temperature difference of the motor over its surroundings. With suitable non-dimensionalization of time the temperature of the motor is given by the differential equation

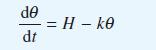
Given that θ = 0 and dθ/dt = 10 when t = 0 and θ = 60 when t = 10 show that

(a) The ultimate rise in temperature is θ = 10/k;

(b) K is a solution of the equation e^–10k = 1 – 6k;

(c)

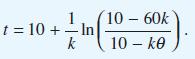
- H = p