Question: Show that Lagranges interpolation formula for cubic interpolation is Use this formula to find a cubic polynomial that fits the function f given in the

Show that Lagrange’s interpolation formula for cubic interpolation is

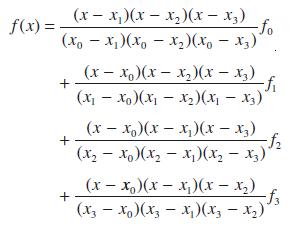
f(x) = (x-x)(x-x)(x (xox)(xox)(x x3) - x) - + (x-x)(x-x)(x - x) + -fi (x - x0)(x - x)(x - x3) -fo

Use this formula to find a cubic polynomial that fits the function f given in the following table:

x fox) -1 - 1 0 0 1 1 2 8

Draw the graph of the cubic for –1 1/3.

f(x) = (x-x)(x-x)(x (xox)(xox)(x x3) - x) - + (x-x)(x-x)(x - x) + -fi (x - x0)(x - x)(x - x3) -fo (x-x)(x-x)(x - x) (x-x)(x-x)(x -$ x3) - (x - x)(x-x)(x - x) -f3 + - (x3 - x)(x3x)(xz - x)`

Step by Step Solution

★★★★★

3.34 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

For cubic interpolation we need four points x i f i ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Engineering Mathematics Questions!

Requirement 1. Complete the payroll register. Round to two decimals. (Round all amounts to the nearest cent. Abbreviations used: Beg. = Beginning; Cum. = Cumulative; Earn. = Earnings; Exp. = Expense;...

Answers are given at the end of these exercises. (a) cos(a + 3) (b) sin(a - 3) = cosa cos sin a cos sin a sin 3 cos a sin 3

QUESTION 5 [20 Marks] "Environmental or green purchasing is the integration of environmental considerations into purchasing policies, programmes, and actions. The objective of green purchasing is to...

Prove or disprove this assertion: Let x',...,x" be all the basic feasible solutions of Axb, x>0; then x is a feasible solution if it is a convex combination x = 0x + + 0NX (0, 0, 0; = 1).

interpolation and the Lagrange polynomial 5. Polynomial Irrte rpolation. {a} Use the Lagrange interpolation process to obtain a polynomial of least degree that assumes these values. 1 I] 2 3 4 y i"...

Match the function with the graph: - -23 - v 24 a. -10-9 -8 - 6 b. . 10 - -6 5 For the polynomial function f(a) = a2 - 3x* + 5, the degree is and the leading coefficient isGiven the polynomial...

EGN 5458: STATISTICAL APPLICATIONS FOR ENGINEERS HOMEWORK 6 Due: 11.02.2023, 08:00 PM Please submit your homework on CANVAS using the assignment page for Homework 6. Please send your homework in ONE...

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

All the information are in it (i) g(x) = x?(x + 5)%(x 1)(x 4) (a) Degree: ; Leading coefficient: ; based on this the end behavior is: (b) the x-intercepts: X-intercept Multiplicity Bounce or cross?...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

What is a slip system in a material? What types of planes and directions tend to be preferred?

Clinical Trial of Bystolic. In clinical trials of the drug Bystolic used to treat hypertension (high blood pressure), 677 Bystolic users were observed for adverse reactions. It was found that among...

if q had a different value, would W / q be different or would it have the same value regardless of the value of q

I pass on all information I receive to my team, as long as it is not confidential. 1. Never 2. Occasionally 3. Frequently 4. Always

Predict the product for each of the following reactions: (a) (b) (c) ? Heat

Î±-Terpinene is a pleasant-smelling compound present in the essential oil of marjoram, a perennial herb. Upon hydrogenation with a metal catalyst, Î±-terpinene reacts with...

Draw all possible conjugated dienes with molecular formula C 6 H 10 , taking special care not to draw the same compound twice.

The management of Zorrilla Corporation is considering dropping product R10C. Data from the company's accounting system appear below: All fixed expenses of the company are fully allocated to products...

consider how far jal instructions can jump

Find the exact solution (s) of the system of equations x^(2)+y^(2)=16 and x=y+4. F(-4,0) and (0,4) H(0,4) and (0,-4) G(4,0) and (-4,0) J(4,0) and (0,-4)