Question: Use Eulers method to compute an approximation X(0.65) to the solution x(0.65) of the initial-value problem using a step size of h = 0.05. dx
Use Euler’s method to compute an approximation X(0.65) to the solution x(0.65) of the initial-value problem
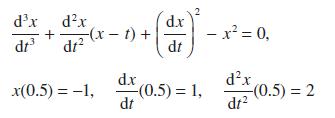
using a step size of h = 0.05.
dx dx + dt dt d.x dt (0.5)=1, (0.5)=2 -(x-t) + x(0.5) = -1, d.x dt - x = 0,
Step by Step Solution
3.48 Rating (161 Votes )
There are 3 Steps involved in it
First we formulate the problem as a set of three coupled firstorder differential equatio... View full answer

Get step-by-step solutions from verified subject matter experts


