The martingale method for portfolio choice, introduced in section 4.1.5, uses the SDF framework to characterize the optimal state-contingent payoffs that agents can attain through financial markets, given their wealth and asset prices, the latter summarized through the SDF. Consider an economy with two dates, \(t=0,1\). At date 0 an agent with wealth \(W\) solves the following optimization problem over his date-1 payoff:

Assume that a riskfree asset is traded, \(1 \in \Xi .{ }^{14}\)

(a) Let \(\lambda\) denote the Lagrange multiplier on the agent's budget constraint, and let \(\hat{X}\) denote the optimal payoff. Show that the agent's first-order condition implies \(\hat{X}=u^{\prime-1}(\lambda M)\).
Show that the optimal payoff for a power-utility investor with \(u(X)=X^{1-\gamma} /\) \((1-\gamma)\) is

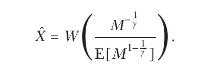
Show that the optimal payoff for a quadratic-utility investor with \(u(X)=-(1 / 2)

\left(X^{b}-ight.\) \(X)^{2}\) is

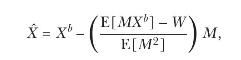
where \(X^{b}>0\) is a constant corresponding to the investor's bliss point. \({ }^{15}\)

(b) The martingale method has traditionally been applied under the assumption of complete markets. In this case, \(X^{*}\) defined in section 4.2.1 is the unique SDF and the optimal payoff formula in part

(a) always yields a feasible (traded) payoff, \(\hat{X} \in \Xi\). When markets are incomplete, however, there exist many valid SDFs. For a general utility function, such as power utility, \(u^{\prime-1}(\lambda M)\) is in \(\Xi\) only for a particular \(M\) that is generically different from \(X^{*}\) and thus hard to pin down. Thus, the martingale method is in general of little use in incomplete-market settings.
An exception is the case of quadratic utility. Show that, under quadratic utility, \(u^{\prime-1}(\lambda M) \in \Xi\) for \(M=X^{*}\).

(c) Express the optimal payoff of a quadratic-utility investor as

where \(1+R^{*} \equiv X^{*} / P\left(X^{*}ight)\) is the gross benchmark return. Explain the intuition behind this condition.

(d) Show that the return to the optimal payoff of a quadratic-utility investor, \(\hat{R}=\) \(\hat{X} / P(\hat{X})-1\), is given by

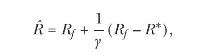
where \(\gamma=\gamma\left(\left(1+R_{f}ight) Wight)\) is the coefficient of relative risk aversion evaluated at a value of consumption that can be obtained by investing all wealth in the riskfree payoff.

(e) Conclude that quadratic-utility investors hold mean-variance efficient portfolios, regardless of the distribution of payoffs.

Data from section 4.1.5

Transcribed Image Text:

max E[u(X)] s.t. W = P(X) = E[MX]. XeE