Return to Fig. 2.25 and prove that if two electromagnetic plane waves making an angle θ have the same amplitude, E₀, the resulting interference pattern on the yx-plane is a cosine-squared irradiance distribution given by

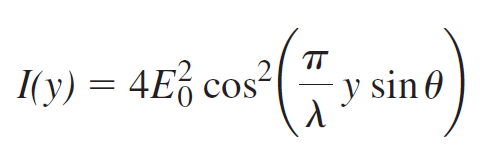
Locate the zeros of irradiance. What is the value of the fringe separation? What happens to the separation as θ increases? Compare your analysis with that leading to Eq. (9.17). Begin with the wave expressions given in Section 2.7, which have the proper phases already worked out, and write them as exponentials.

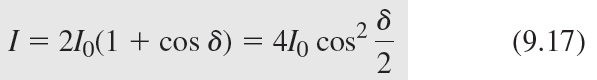
Fig. 2.25

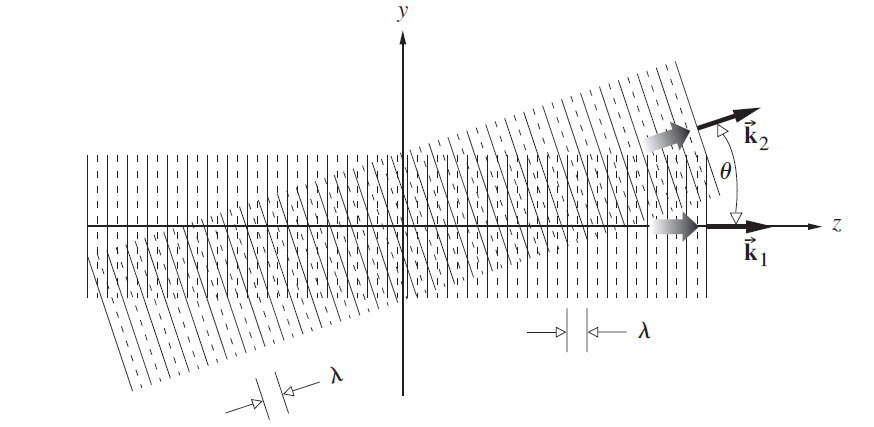
I(y) = 4E% cos TT .2 y sin0 I = 210(1 + cos 8) = 4lo cos- 2 (9.17)