The bisection method applies to onedimensional convex problems of the form where x l < x u are both finite, and f : R

The bisection method applies to onedimensional convex problems of the form

where x_l u are both finite, and f : R → R is convex. The algorithm is initialized with the upper and lower bounds on x: x = x_l , x̅ = x_u, and the initial x is set as the midpoint

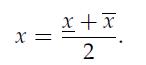
Then, the algorithm updates the bounds as follows: a sub-gradient g of f at x is evaluated; if g

1. Show that the bisection method locates a solution x* within accuracy ϵ in at most log₂(x_u – x_l)/ϵ – 1 steps.

2. Propose a variant of the bisection method for solving the unconstrained problem minx f (x), for convex f .
3. Write a code to solve the problem with the specific class of functions f : R → R, with values

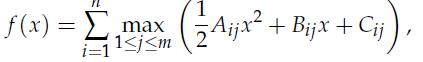
where A, B, C are given n x m matrices, with every element of A non-negative.

min f(x) x x xu < < : x