In this exercise we introduce some “equivalent” formulations of a system of linear equations and then study a linear recursive algorithm for solution of this system.

Ax = b, A ∈ R^m,n,

1. Consider the system of linear equations where A† is any pseudoinverse of A (that is, a matrix such that AA†A = A). Prove that (7.8) always admits a solution. Show that every solution of equations (7.7) is also a solution for (7.8). Conversely, prove that if b 2 R(A), then every solution to (7.8) is also a solution for (7.7).

where A^† is any pseudoinverse of A (that is, a matrix such that AA^†A = A). Prove that (7.8) always admits a solution. Show that every solution of equations (7.7) is also a solution for (7.8). Conversely, prove that if b ∈ R(A), then every solution to (7.8) is also a solution for (7.7).

2. Let R ∈ R^n,m be any matrix such that N(RA) = N(A). Prove that    

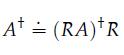
is indeed a pseudoinverse of A.

3. Consider the system of linear equations RAx = Rb,

4. Under the setup of the previous point, consider the following linear iterations: for k = 0, 1, . . .,

5. Suppose A is positive definite Discuss how to find a suitable scalar α and matrix R ∈ R^n,n satisfying the conditions of point 3., and such that the iterations (7.10) converge to a solution of (7.9).

6.

Ax = AAb,