Consider linear iterations of the form

where F ∈ R^n,n, c ∈ Rⁿ, and the iterations are initialized with x(0) = x₀. We assume that the iterations admit a stationary point, i.e., that there exist x? ∈ Rⁿ such that

In this exercise, we derive conditions under which x(k) tends to a finite limit for k → ∞. We shall use these results in Exercise 7.7, to set up a linear iterative algorithm for solving systems of linear equations.

1. Show that the following expressions hold for all k = 0, 1, . . .:

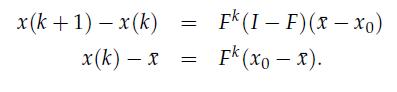
2.

x(k+1) = Fx (k)+c, k = 0,1,...,