In this exercise, we revisit Exercise 9.3, and approach it using the S-procedure of Section 11.3.3.1.

1. Show that the minimum distance from the line segment L to the origin is above a given number R ≥ 0 if and only if

2. Apply the S-procedure, and prove that the above is in turn equivalent to the LMI in

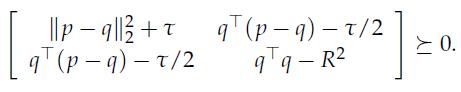
3. Using the Schur complement rule¹⁵, show that the above is consistent with the result given in Exercise 9.3.

Section 11.3.3.1:

The S-procedure. The so-called S-procedure establishes an equivalence between a certain LMI condition and an implication between two quadratic functions. More precisely, let f₀(x), f₁(x) be two quadratic functions:

 

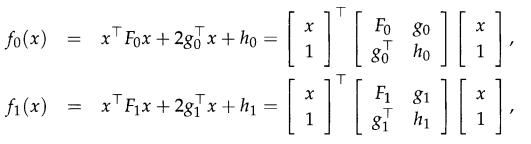
||^ (p q ) + q ||2 R whenever A(1-1) 0.