The following problem is known as Robust Principal Component Analysis: where * stands for the nuclear norm, and 1 here denotes the sum of

The following problem is known as Robust Principal Component Analysis:

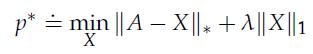
where ІІ·ІІ* stands for the nuclear norm, and ІІ·ІІ₁ here denotes the sum of the absolute values of the elements of a matrix. The interpre-tation is the following: A is a given data matrix and we would like to decompose it as a sum of a low rank matrix and a sparse matrix. The nuclear norm and ℓ₁ norm penalties are respective convex heuristics for these two properties. At optimum, X* will be the sparse component and A – X* will be the low rank component such that their sum gives A.

1. Find a dual for this problem.

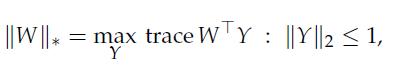
where ΙΙ · ΙΙ₂ is the largest singular value norm.

2. Transform the primal or dual problem into a known programming class (i.e. LP, SOCP, SDP etc.). Determine the number of variables and constraints.

where I is the identity matrix.

3. Using the dual, show that when λ > 1, the optimal solution is the zero matrix.

p* = min || A - X||* + A||X||1