Question: In this exercise, you derive a bound on the largest absolute value of the derivative of a polynomial of a given order, in terms of

In this exercise, you derive a bound on the largest absolute value of the derivative of a polynomial of a given order, in terms of the size of the coefficients¹. For ω ∈ R^k+1, we define the polynomial p_ω, with values

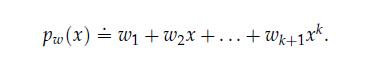
Pw (x) = W + Wx + ... + Wk+1xk.

Show that, for any p ≥ 1

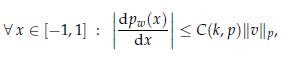
where ν = (ω₂, . . . ,ω_k+1) ∈ R^k, and

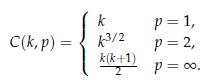
Pw (x) = W + Wx + ... + Wk+1xk.

Step by Step Solution

★★★★★

3.45 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

We have with z 1 2 k and u... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Optimization Models Questions!

You are a consultant who has been hired to help the province of Nova Scotia establish regu- lations for commercial cod fishing in their territorial waters. The problem is that you never actually know...

In this exercise you will see how matrix multiplication can be used to get a nice proof of the major identities that play a role in the extended Euclidean algorithm. We consider two integers a, b e Z...

In this exercise you will prove Theorem 9.8.2. a. Prove that the joint p.d.f. of the data given the parameters 1, 2, and can be written as a constant times b. Multiply the prior p.d.f. times the...

Accuracy in Matlab and Condition Number For most systems of linear equations, we can get an answer with enough accuracy fast enough in a number of different ways, and we don't even bother with trying...

Using MATLAB ML2.txt file: 164 1976 684 27824 9180 4580 20 16604 66260 43956 39547 1577 109 7861 511 3811 24721 14519 60221 11 9402 18 6150 240 582 3828 2238 13806 1206 78 8388 29979 13441 516 1269...

Please use MATLAB (add comments) Importing, Sorting, Fitting, and Exporting Data Write a program that loads a 1010 array of numbers from the data file (ML2.txt) given on Canvas and sorts that data...

b) Write a function defined as: def MatrixProductSmallerThan (A, val): A: a FULL matrix (list of lists) containing integers or floats val: a float or integer. return value: the product of the terms...

Dear Sir I Would like the answers of the documents i attach School of Business and Economics EXAM Course : Code : Date Time Location Risk Management EBC4056 : 3 June, 2010 : 9.00 - 12.00 : MECC...

Objectives 1. Understand the design, implementation, usage and limitation of ADT based on fixed- sized arrays. 2. Gain experience implementing abstract data types using already developed data...

I need help with implementing the functions in the header file in C++ Implement Class "polynomial" with a Linked List // FILE: poly2.h // CLASS PROVIDED: // class polynomial (in the namespace...

For each DE in problems solve analytically to obtain solution curves through the point (1,1) and (-1,-1), Then using an appropriate software package draw the direction field and superimpose your...

Product Sales When the points in a scatter plot show a curvilinear trend rather than a linear trend, statisticians have methods of fitting curves rather than straight lines to the data, thus...

f . Find the PV of an ordinary annuity that pays $ 1 , 0 0 0 each of the next 4 years if the interest rate is 1 8 % . Then find the FV of that same annuity. Round your answers to the nearest cent. PV...

3.3 Identify five primary ways in which words have power. PRINCIPLE POINTS: Words are extremely powerful. They can create and label our experiences, communicate our feelings, affect our thoughts and...

Are the events A 1 = {mother has influenza} and A 2 = {father has influenza} independent? Suppose an influenza epidemic strikes a city. In 10% of families the mother has influenza; in 10% of families...

What is the probability that at least one child will get influenza? Suppose an influenza epidemic strikes a city. In 10% of families the mother has influenza; in 10% of families the father has...

Based on Problem 3.12, what is the conditional probability that the father has influenza given that the mother has influenza? Suppose an influenza epidemic strikes a city. In 10% of families the...

d) 3. A) Provide the methods used to compute a bank's ROA and ROE. (10 pts) bl boblongo s2rs Deup gnlvello s ROE= ROA= B) If a bank reduces the amount of its capital in half and ROA stays constant,...

Madam Zurin is the Financial Manager of DDNK Bhd. She is responsible of identifying the lowest possible cost of raising capital for new projects to be undertaken by the company. DDNK Bhd has been...

The Sisyphean Company has a bond outstanding with a face value of $1,000 that reaches maturity in 15 years. The bond certificate indicates that the stated coupon rate for this bond is 9.9% and that...