Let A = (a_ij) ∈ R^n,n, b ∈ Rⁿ, with a_ii ≠ 0 for every i = 1, . . . , n. The Jacobi method for solving the square linear system Ax = b consists in decomposing A as a sum: A = D + R, where D = diag (a₁₁, . . . , a_nn), and R contains the off-diagonal elements of A, and then applying the recursion

with initial point

The method is part of a class of methods known as matrix splitting, where A is decomposed as a sum of a “simple,” invertible matrix and another matrix; the Jacobi method uses a particular splitting of A. 

1. Find conditions on D, R that guarantee convergence from an arbitrary initial point.

2. The matrix A is said to be strictly row diagonally dominant if

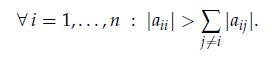
Show that when A is strictly row diagonally dominant, the Jacobi method converges.

x(k+1) = D(b - Rx(k)), k = 0,1,2,...,