Question: Let A S n + be a symmetric, positive semi-definite matrix. 1. Show that the trace, trace A, and the Frobenius norm,A F, de-pend

Let A ∈ Sⁿ₊be a symmetric, positive semi-definite matrix.

1. Show that the trace, trace A, and the Frobenius norm,ΙΙAΙΙ_F,de-pend only its eigenvalues, and express both in terms of the vector of eigenvalues.

2. Show that

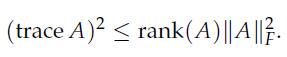
(trace A) rank(A)||A||} .

3. Identify classes of matrices for which the corresponding lower bound on the rank is attained.

(trace A) rank(A)||A||} .

Step by Step Solution

★★★★★

3.40 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

1 2 The rank of A is simply the number of eigenvalues that are nonzero Without loss of generality we assume that the eigenvalues are ordered in decreasing fashion The inequality follows from the CauchySchwartz inequality with 1 r the vector of ones in R r we have which proves the desired result 3 We begin with an eigenvalue ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Optimization Models Questions!

Let Sn be a covariance matrix satisfying the hypotheses of Theorem 8.6. To prove Theorem 8.7, proceed as follows: (a) Show that the trace of Sn is the total variance. (See Section 1.3, Exercise 43,...

The trace of a square matrix is the sum of its diagonal entries. (a) Find the formula for the characteristic polynomial of a 2 2 matrix. (b) Show that trace is invariant under similarity, and so we...

Create a conclusion to following work. Hotels form an uninterrupted narrative of a story, filling guests with emotions that define their stay. They have ceased to be considered one-dimensional places...

Exercise 4.9 (A lower bound on the rank) Let A c S" be a symmet- ric, positive semidefinite matrix. 1. Show that the trace, trace A, and the Frobenius norm, A|F, de- pend only on its eigenvalues, and...

Applied Mathematics and Computation 95 (1998) 181192 Love dynamics: The case of linear couples Sergio Rinaldi 1 Centro Teoria dei Sistemi, CNR, Politecnico di Milano, Via Ponzio 34/5, 20133 Milan,...

b. This problems uses a matrix inner product and norm (the inner product simplifies when A is symmetric) (A,B) := Tr(A"B), || A|| = V Tr(A' A) Set C = S as the positive semi-definite matrices, and...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

For monotone functions f, f0: P Q between posets (P, vP ) and (Q, vQ), let f v f(i) Prove that the binary relation v is a partial order. [3 marks] (ii) For monotone functions between posets p : P 0...

Show the parse trees for the two parses that the grammar assigns for sentence S1. S1: the train station bus rumbles [3 marks] (b) Give an algorithm for a bottom-up passive chart parser without...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

You are presented with the following information Starter Profit and loss account for the year to 31 March 2012 Sales 10000 Purchases 5000 Less Closing stock 1000 4000 Gross profit 6000 Less...

The average of five numbers is 58. The average of the first two numbers is 48.5 and the average of last two numbers is 53.5. What is the third number?

Part 6: Prepare the journal entry to record the completion of any job(s) during the month. (List all debit entries before credit entries. Credit account titles are automatically indented when amount...

Choose twosocialmediawebsites.Pulluptheirprivacypoliciesandanswer the followingquestionsforeach. a. What informationwillbecollectedaboutyou? b. How...

If the population tested is representative of the general population, then what are the PV+ and PV using this test? Hypertension Laboratory measures of cardiovascular reactivity are receiving...

Does there seem to be any difference in the effect of the antibiotics on clearance of otitis media? Express your results in terms of relative risk (RR). Consider separate analyses for unilateral and...

The investigators recorded the ages of the children because they felt this might be an important factor in determining outcome. Were they right? Try to express your results in terms of RR. Table 3.12...

Assume that the company expects to sell 20,500 units next month. Prepare two contribution format income statements, one assuming that operations are not automated and one assuming that they are.

An investment of $86 generates after-tax cash flows of $47 in Year 1, $62 in Year 2, and $150 in Year 3. The required rate of return is 20 percent. The net present value is closest to? (Please show...

Meade Nuptial Bakery makes very elaborate wedding cakes to order. The company has an activity-based costing system with three activity cost pools. The activity rate for the Size-Related activity cost...