Let x_i, i = 1, . . . , n, be given real numbers, which we assume without loss of generality to be ordered as x₁ ≤ x₂ ≤ _.........≤ x_n, and consider the scalar equation in variable n that we encountered in Section 12.3.3.3:

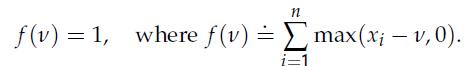
1. Show that f is continuous and strictly decreasing for ν ≤ x_n.

2. Show that a solution ν* to this equation exists, it is unique, and it must belong to the interval

3. This scalar equation could be easily solved for n using, e.g., the bisection method. Describe a simpler, “closed-form” method for finding the optimal n.

n f(v) = 1, where f(v) = [max(x - v, 0). i=1