We consider the following problem in a symmetric n x n matrix variable X where is an empirical covariance matrix,X 1 denotes the sum of

We consider the following problem in a symmetric n x n matrix variable X

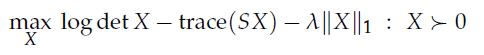
where is an empirical covariance matrix,ΙΙXΙΙ₁ denotes the sum of the absolute values of the elements of the positive definite matrix X, and λ > 0 encourages the sparsity in the solution X. The problem arises when fitting a multivariate Gaussian graphical model to data. The ℓ₁-norm penalty encourages the random variables in the model to become conditionally independent.

1. Show that the dual of the problem takes the form

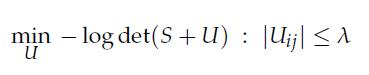
2. We employ a block-coordinate descent method to solve the dual.
Show that if we optimize over one column and row of U at a time, we obtain a subproblem of the form

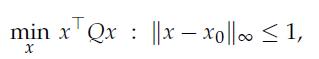
3. Show how you can solve the constrained QP problem above using following methods. Make sure to state precisely the algorithm’s steps.

• Coordinate descent.
• Dual coordinate ascent.
• Projected subgradient.

• Projected subgradient method for the dual.
• Interior-point method (any flavor will do).

Compare the performance (e.g., theoretical complexity, running time/convergence time on synthetic data) of these methods.

4. Solve the problem (using block-coordinate descent with 5 updates of each row/column, each step requiring the solution of the QP above) for a data file of your choice. Experiment with different values of l, report on the graphical model obtained.

max log det X - trace (SX) - A||X||1: X>0 X