In Section 13.2, we examined the problem of fitting a polynomial of degree d through m data points (u_i, y_i) ∈ R², i = 1, . . . ,m. Without loss of generality, we assume that the input satisfies Ιu_iΙ ≤ 1, i = 1, . . . ,m. We parametrize a polynomial of degree d via its coefficients:

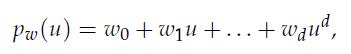
where w ∈ R^d+1.

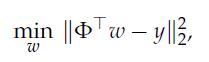
where the matrix Φ has columnsAs detailed in Section 13.2.3, in practice it is desirable to encourage polynomials that are not too rapidly varying over the interval of interest. To that end, we modify the above problem as follows:

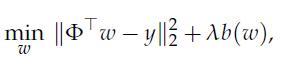
where λ > 0 is a regularization parameter, and b(ω) is a bound on the size of the derivative of the polynomial over [–1, 1]:

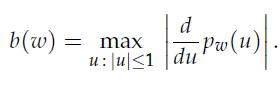
1. Is the penalty function b convex? Is it a norm?
2. Explain how to compute a subgradient of b at a point w.
3. Use your result to code a subgradient method for solving problem (12.33).

Pw (u) = wo+wu+...+wad,