The line segment linking two points p, q R n (with p q) is the set = {p + (1 )q :

The line segment linking two points p, q ∈ Rⁿ (with p ≠ q) is the set  = {λp + (1 – λ)q : 0 ≤ λ ≤ 1.

1. Show that the minimum distance D* from a point a ∈ Rⁿ to the line segment  can be written as a QP in one variable

for appropriate vectors c, d, which you will determine.

2. Prove that the minimum distance is given by

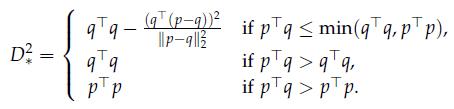
3. Interpret the result geometrically.