For a given vector R n , the average can be found as the solution to the optimization problem where 1 is the

For a given vector ν ∈ Rⁿ, the average can be found as the solution to the optimization problem

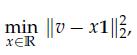
where 1 is the vector of ones in Rⁿ. Similarly, it turns out that the median (any value x such that there is an equal number of values in v above or below x) can be found via

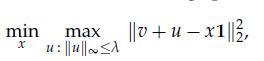
in which we assume that the components of v can be independently perturbed by a vector u whose magnitude is bounded by a given number λ ≥ 0.

1. Is the robust problem (9.18) convex? Justify your answer precisely, based on expression (9.18), and without further manipulation.
2. Show that problem (9.18) can be expressed as

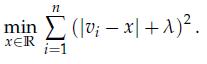
3. Express the problem as a QP. State precisely the variables, and constraints if any.
4. Show that when λ is large, the solution set approaches that of the median problem (9.17).
5. It is often said that the median is a more robust notion of “middle” value than the average, when noise is present in ν. Based on the previous part, justify this statement.

min ||v- x1||3, XER