In this problem, you will derive the equations used to explain the Michelson interferometer for incident light of a single frequency.

a. Show that the expression

represents the sum of two waves of the form (A₀ / ˆš2)exp[i(k x ˆ’ω t)], one of which is phase shifted by the amount δ (t) evaluated at the position y _D.

b. Show using the definition I (t) = A(t)A^*(t) that I (t) = I₀ [2(1 + cos δ (t))]

c. Expressing δ (t) in terms of Δd (t), show that

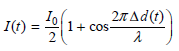
d. Expressing Δd (t) in terms of the mirror velocity v, show that

A) = 20 A(t) = (1 + e5())exp[i(kyp wt)] %3D I(t) = 2 16) = 2T4() 1+ cos