Let€™s look in more detail at how a satellite is moved from one circular orbit to another. FIGURE CP13.71 shows two circular orbits, of radii r₁and r₂, and an elliptical orbit that connects them. Points 1 and 2 are at the ends of the semi major axis of the ellipse.

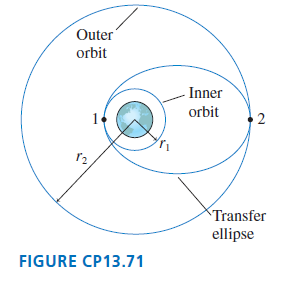a. A satellite moving along the elliptical orbit has to satisfy two conservation laws. Use these two laws to prove that the velocities at points 1 and 2 are

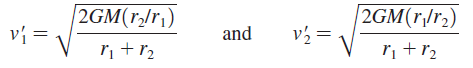
The prime indicates that these are the velocities on the elliptical orbit. Both reduce to Equation 13.22 if r₁ = r₂ = r.
b. Consider a 1000 kg communications satellite that needs to be boosted from an orbit 300 km above the earth to a geosynchronous orbit 35,900 km above the earth. Find the velocity v₁ on the inner circular orbit and the velocity v'₁ at the low point on the elliptical orbit that spans the two circular orbits.
c. How much work must the rocket motor do to transfer the satellite from the circular orbit to the elliptical orbit?
d. Now find the velocity v'₂ at the high point of the elliptical orbit and the velocity v₂ of the outer circular orbit.
e. How much work must the rocket motor do to transfer the satellite from the elliptical orbit to the outer circular orbit?
f. Compute the total work done and compare your answer to the result of Example 13.6.

Outer orbit Inner orbit Transfer ellipse FIGURE CP13.71 2GM(r,/r) vi = ri +r2 2GM(r,lr2) v = and ri+r2