1. Using the spreadsheet model from Case 2.1 as a starting point, use Solver to find the...

Question:

1. Using the spreadsheet model from Case 2.1 as a starting point, use Solver to find the optimal set of projects to approve. The solution should maximize the total NPV from the approved projects, and it should satisfy the constraints imposed by CEO J. R. Bayer and the functional areas: (1) capital expenditures over the three years should not exceed $10 billion; (2) capital expenditures in any single year should not exceed $4 billion; and (3) at least one project must be approved for each functional area.

2. Cliff looks at the optimal solution from question 1 and sees that it is under budget in each year and in total for all three years. This seems to be a good sign, and he interprets it to mean that the budget limitations aren't important after all. Explain why his interpretation is wrong. Then use SolverTable to help him see how NPV could increase with larger budgets. Specifically, vary each of the four budget limits in question 1 (total budget, bud-get for year 1, budget for year 2, and budget for year 3) in separate SolverTable runs over reasonable ranges.

3. Continuing question 2, let all four of the budgets increase by the same percentage in another SolverTable run. (You can choose the range of percentage increases.) What effect does this have on the total NPV?

4. The solution in question 1 still might not satisfy the functional areas. They will each get at least one project, but they will probably want more. Find the implications of promising each functional area at least two projects.

5. Another aspect of the solution in question 1 bothers Cliff. He believes it is approving too many joint partnerships. Use SolverTable to find the implications of limiting the number of joint partnerships to n, where n can vary from 3 to 6.

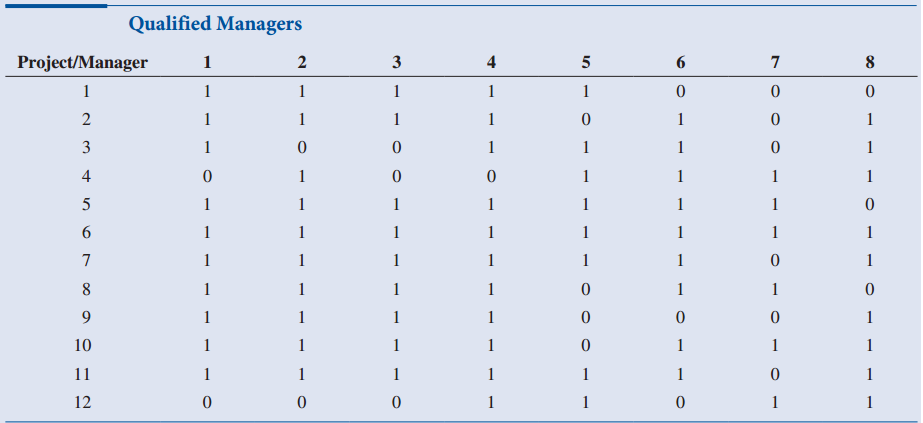
6. One aspect of the problem that has been ignored to this point is that each approved project must be led by a senior project man-ager. Cliff has identified only eight senior managers who qualify and are available, and each of these can manage at most one project. In addition, some of these managers are not qualified to manage some projects. This in-formation is summarized in Table 6.12, where 1 indicates that the manager is qualified for the project and 0 indicates otherwise. The company's problem is the same as before, but now extra decisions have to be made: which manager should be assigned to each approved project? Of course, a project can't be approved unless a qualified manager is assigned to it.

This is an extension of Case 2.1 from Chapter 2, so you should read that case first. It asks you to develop a spreadsheet model using a 0-1 variable for each potential project so that Cliff Erland, Manager for Project Development, can easily see the implications of approving any set of projects. Cliff would now like you to find the optimal set of projects to approve. Specifically, he has asked you to do the following. Summarize all of your results in a concise memo.

Table 6.12:

Data from Case 2.1:

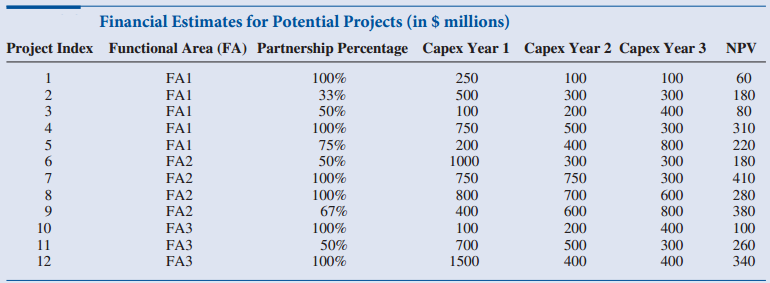
Ewing Natural Gas is a large energy company with headquarters in Dallas, Texas. The company offers a wide variety of energy products and has annual revenues of approximately $50 billion. Because of the diverse nature of the company, its Manager for Project Development, Cliff Erland, is under continual pressure to manage project proposals from the functional areas of the company. At any point in time, there might be dozens of projects at various stages requiring a wide variety of capital expenditures, promising widely varying future revenue streams, and containing varying degrees of risk. Cliff has a difficult balancing act. The company's CEO, J.R. Bayer, is very concerned about keeping capital expenditures within a fixed budget and managing risk. The heads of the company's functional areas are less worried about budgets and risks; they are most concerned that their pet projects are approved. Cliff also knows that many of the proposed projects, especially those requiring large capital expenditures, must be led by senior project managers with the appropriate experience and skills, and he is keenly aware that the company has only a limited supply of such managers. Cliff is currently about to meet with all parties involved to discuss project proposals for the next three years. He has proposals from the various functional areas for projects they would like to undertake. Each of these is accompanied by a schedule of capital expenditures over the next three years and a financial analysis of the expected revenue streams. These lead to an NPV for each proposal, using the company's hurdle rate of 12%. (Table 2.2.) J.R. Bayer has stated in no uncertain terms that the total of capital expenditures for the approved projects can be no more than $10 billion and that no more than $4 billion should be spent in any single year. Unfortunately, the capital expenditures for the potential list of projects is well over $10 billion, so Cliff knows that some of these very promising projects will not be approved. Before the big meeting, Cliff wants to be thoroughly prepared to answer all of the questions he knows he will be asked by the CEO, the functional heads, and other interested parties. As a first step, he wants you to develop an Excel spreadsheet model that provides the following. (You will be asked to extend this analysis in cases in later chapters.)

Table 2.2: