Question: Show that Let S = 1 + 2 + ... + (n - 1) + n S = n + (n - 1) + (n

Show that 

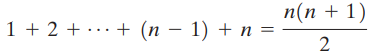
п(п + 1) |1 + 2 +... + (n — 1) + п %3


Let

S = 1 + 2 + ... + (n - 1) + n 

S = n + (n - 1) + (n - 2) + ... + 1 


Add these equations. Then 

25 = [1+ n] + [2 + (n – 1)] + · · · + [n + 1] n terms in brackets

Now, complete the derivation.


( + 1) |1 + 2 +... + (n 1) + %3 25 = [1+ n] + [2 + (n 1)] + + [n + 1] n terms in brackets

Step by Step Solution

★★★★★

3.46 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

nn1 To show that 123n1n 2 Let S1 2 3 ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Q:

Show that if and only if there is a sequence 0 0, there exists N = N (e) such that k and n imply (| X k X | e) (| X k X | e k )...

Q:

Show that (9) in Sec. 12.6 with coefficients (10) is a solution of the heat equation for t > 0 assuming that f(x) is continuous on the interval 0 ¤ x ¤ L and has one-sided derivatives...

Q:

Consider the measurable space (W, A) and let A n A, n = 1, 2, then recall that And (i) Show that A n A n . (If also A n A n so that A n = n A n then this set is denoted by A n and is called the...

Q:

Let Xi,i = 1, 2,..., n be a random sample of size n drawn from a population of size N with population distribution given by f (x) = 1 2 e (x)2 22 ,

Q:

The 0-1 knapsack problem is the following: a thief robbing a store finds n items. The ith item is worth v_i dollars and weighs w_i kilos with i and w_i positive integers. The thief wants to take as...

Q:

Let S(n) = 1 + 2 +???..+ n be the sum of the first n natural numbers and let C(n) =13 + 23 + - + n3 be the sum of the first n cubes. Prove the following equalities by induction on n, to arrive at the...

Q:

We will consider the set X" = Z, as a discretization of the circle. Let | be the real vector space of functions on X, i.e. V = R. Let B = (e1, ..., en) be the basis of / defined by e;([k]) = 1 if [k]...

Q:

Q5 (4 points) We will consider the set X.= Z, as a discretization of the circle. Let V be the real vector space of functions on X, i.e. V = RX . Let B = (e1, ... , en) be the basis of V defined by...

Q:

Let S(n) = 1 + 2 + + n be the sum of the first n natural numbers, and let C(n) = 13 + 23 + + n3 be the sum of the first n cubes. Prove the following equalities by induction on n: (a) S(n) = 1/2*n(n +...

Q:

Let S(n) = 1 + 2 + + n be the sum of the first n natural numbers and let C(n) = 1 3 + 2 3 + + n 3 be the sum of the first n cubes. Prove the following equalities by induction on n, to arrive at...

Q:

Nuwan has invested a $30 000 insurance settlement to earn interest at 4.18% compounded semi-annually for the next 10 years. If he then makes withdrawals of $850 at the beginning of every 3 months...

Q:

Briefly describe how the percentiles are calculated for a data set.

Q:

Date Number of units Cost per unit Total cost November 1 Inventory, beginning 6 0 0 $ 2 0 . 2 5 $ 1 2 , 1 5 0 November 1 5 Purchase 1 , 0 0 0 $ 2 0 . 2 6 $ 2 0 , 2 6 0 November 2 4 Purchase 3 0 0 $ 2...

Q:

8. Nigerias 2001 GNP per capita was $290, more than one and one-half times that of neighboring Nigers $180. What other assessments of socioeconomic welfare (other than GNP per capita in U.S. dollars...

Q:

For the following exercises, evaluate the binomial coefficient. (7)

Q:

For the following exercises, find the common ratio for the geometric sequence. 0.125, 0.25, 0.5, 1, 2, ...

Q:

Is the sequence 2, 1, 1/2 , 1/4 , geometric? If so find the common ratio. If not, explain why.

Q:

3. 0.25/1.25 points | Previous Answers LCalcCon5 6.4.013. My Notes Ask Your Teacher The willingness of saddle producers to supply saddles can be modeled as for p

Q:

Need explanation, answers, six step hypothesis test, along with minitab answers and instructions. This question is based on the 2020 Annual Surveys of Community. A test has been conducted with the...

Q:

Here are data on two stocks, both of which have discount rates of 15%: Stock A Stock B Return on equity 15 % 12 % Earnings per share $ 3.00 $ 2.30 Dividends per share $ 1.80 $ 1.80 a. What are the...