Question: Given the Gaussian random variable with the pdf where Ï > 0 is the standard deviation. If Y = X 2 , find the pdf
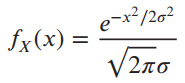
where σ > 0 is the standard deviation. If Y = X2, find the pdf of Y. Note that Y = X2 is symmetrical about X = 0 and that it is impossible for Y to be less than zero.
e-x/2o? fx(x) = V2
Step by Step Solution
3.46 Rating (166 Votes )
There are 3 Steps involved in it
The result i... View full answer

Get step-by-step solutions from verified subject matter experts


