A Poisson process is a real-valued stochastic process (left(N_{t} ight)_{t geqslant 0}) such that (N_{0}=0), (N_{t}-N_{s} sim N_{t-s}) and for (t_{0}=0 0). In particular, (left(N_{t}

A Poisson process is a real-valued stochastic process \(\left(N_{t}\right)_{t \geqslant 0}\) such that \(N_{0}=0\), \(N_{t}-N_{s} \sim N_{t-s}\) and for \(t_{0}=00\). In particular, \(\left(N_{t}\right)_{t \geqslant 0}\) satisfies (B0), (B1), (B2).

a) Show that the process \(\left(N_{t}\right)_{t \geqslant 0}\) does not satisfy the assumptions of the Kolmogorov-Slutsky-Chentsov theorem, Theorem 10.1.

b) Show that (10.1) holds true for \(n=1, \alpha>0\) and \(\beta=0\). Discuss the role of \(\beta\) for Theorem 10.1.

c) Let \(\lambda=1\). Determine for the process \(X_{t}=N_{t}-t\) the mean value \(m(t)\) and the covariance \(C(s, t)=\mathbb{E}\left(X_{s} X_{t}\right), s, t \geqslant 0\).

Data From  Theorem 10.1

Data From (10.1)

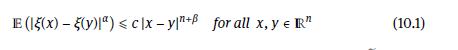
10.1 Theorem (Kolmogorov 1934; Slutsky 1937; Chentsov 1956). Denote by ((x))XER a stochastic process on (Q, A, P) with values in Rd and index set R". If E ((x)-(y))