Consider theM/M/1 queueing model, and denote by T the amount of time a randomly chosen customer spends in the system. We consider the stationary regime and take for granted that the r.v. K, the number of customers that are ahead of a newly arriving customer, has the same distribution as X_t in the stationary regime.

(a) Give a heuristic argument that in the stationary regime,

provided μ> λ. Comment on the fact that E{T} → ∞ as λ is approaching μ. (A new customer should wait for K +1 services to be completed: K for the customers ahead, and one more for her/himself. The mean time of each service is 1/μ.

(b) Find the expecting waiting time E{T} in the situation of Exercise 16.

(c) When writing that E{T} = 1/μE{K+1}, we had to justify this step because, as a matter of fact, T is the sum of a random number of r.v.’s; namely,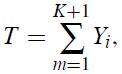

where Y_i are exponential r.v.’s. Realize that to make the proof of (3.1) rigorous, we may use the result of Example 3.6.2-1.