The system considered in example 9.7 is generalized as follows: If the system makes a direct transition from state 0 to the blocking state 2 , then the subsequent renewal time is exponential with parameter \(\mu_{0}\). If the system makes a transition from state 1 to state 2 , then the subsequent renewal time is exponential with parameter \(\mu_{1}\).

(1) Model the system by a Markov chain and draw the transition graph.

(2) What is the stationary probability that the system is blocked?

Data from Example 9.7

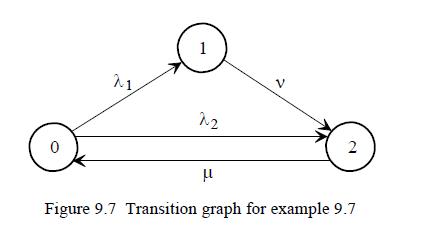
Example 9.7 A system has two different failure types: type 1 and type 2. After a type i-failure the system is said to be in failure state i; i = 1,2. The time L; to a type i-failure is assumed to have an exponential distribution with parameter ;, and the random variables L1 and L2 are assumed to be independent. Thus, if at time t = 0 a new system starts working, the time to its first failure is Yo = min(L1,L2). After a type 1-failure, the system is switched from failure state 1 into failure state 2. The time required for this is exponentially distributed with parameter v. After entering failure state 2, the renewal of the system begins. A renewed system immediately starts working. The renewal time is exponentially distributed with parameter u. This process continues to infinity. All life- and renewal times as well as switching times are assumed to be independent. This model is, for example, of importance in traffic safety engineering: When the red signal in a traffic light fails (type 1-failure), then the whole traffic light is switched off (type 2-failure). That is, a dangerous failure state is removed by inducing a blocking failure state.