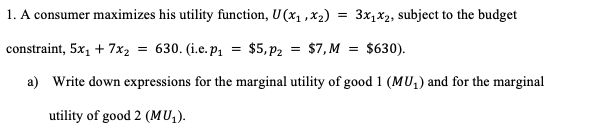
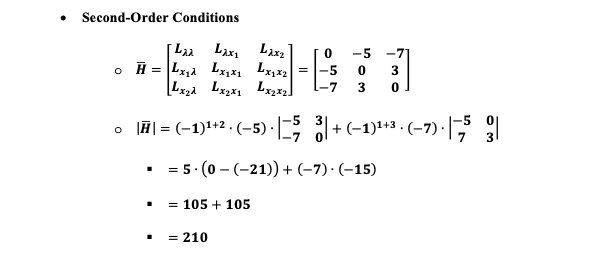
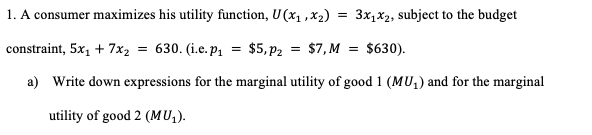
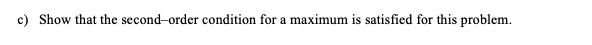
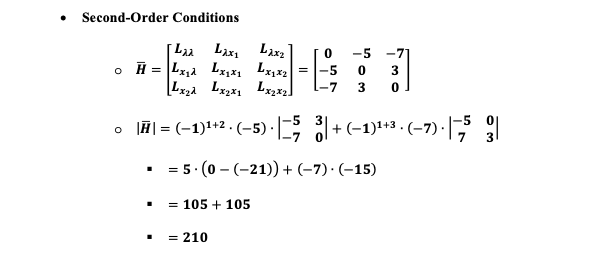
1. A consumer maximizes his utility function, U(x, , x2) = 3x1x2, subject to the budget constraint, 5x1 + 7x2 = 630. (i.e.p, = $5, p2 = $7, M = $630). a) Write down expressions for the marginal utility of good 1 (MU, ) and for the marginal utility of good 2 (MU,).b) Set up the Lagrangian function, write down the first-order necessary conditions for a solution to the consumer's problem, and find the values of x1 and x2 that satisfy those conditions.c) Show that the second-order condition for a maximum is satisfied for this problem.du . MU= = 3x2 dx1 du . MU= = 3x1 dx2Lagrangian function o [ = 3x X2 + 1(630 - 5x1 - 7x2) . First Order Conditions (FOC) O 0 5x1 - 3x2 - 51 = 0 o 3x2 = 51 0 1= =O -=U 8x2 . 3x1 - 71 =0 0 3x1 = 71 o 1 = =x1 O = 0 . 630- 5x1 - 7x2 = 0 . Set 1 equal to each other o xz = =x1 O X2 = X1 . Replace x2 in s = = 0 to solve for X1 0 630 - 5x1 -7 (x1) =0 0 630 -10x1 = 0 0 630 = 10x1 o xi = 63 . Replace x, with x; to solve for x2 0 x2 = ; (63) 0 x2 = 45 . Plug in x; to solve for 2* o 1 = (63) o 1' = 27. Second-Order Conditions Lax LAxi Laxz -5 3 H = Lxd Lxx1 Lx1X2 = -5 0 3 0 Lxzd LxZKI LxaxZ 7 o HI = (-1)1+2 . (-5) . 3 8+(-1)1+3 . (-7). 2 . = 5 . (0 - (-21)) + (-7) . (-15) = 105 + 105 = 210