1)

clc

clear all

close all

A = 0.01; % m^2

E = 60*10^9; % Pa

F = 7*10^6; % N

node = 6; % No- of nodes

DOF = 2; % DOF

TDOF = node*DOF; % Total DOF

coord = [0,0;0,8;4,4;6,2;8,0;4,0]; % coordinate of Nodes

Nelem = 9;

Elcon = [1,2;1,3;1,6;2,3;3,4;3,6;4,5;4,6;5,6]; % conecting elements

BCS=zeros(TDOF,DOF); % ?????

BCS(1,1)=1;

BCS(2,1)=1;

BCS(3,1)=1;

BCS(4,1)=1;

BCS(11,1)=1;

BCS(12,1)=1;

Ksys= zeros(TDOF,TDOF);

figure

hold on

for ielem=1:Nelem

line([coord(Elcon(ielem,1),1),coord(Elcon(ielem,2),1)],[coord(Elcon(ielem,1),2),

coord(Elcon(ielem,2),2)],'linestyle','-')

end

xlabel({'Position x'});

ylabel({'Position Y'});

% build the ss stiffenis matrix

for ielem = 1: Nelem

node1 = Elcon(ielem,1);

node2 = Elcon(ielem,2);

dx=coord(node2,1)-coord(node1,1);

dy=coord(node2,2)-coord(node1,2);

L=sqrt(dx^2+dy^2);

c=dx/L;

s=dy/L;

T1=[c,s;-s,c];

% initilize the transformation matrix

T=zeros(4);

T(1:2,1:2)=T1;

T(3:4,3:4)=T1;

% stiffness matrix m local coordinate sys

K=(A*E/L)*[1,0,-1,0 ; 0,0,0,0 ; -1,0,1,0 ; 0,0,0,0];

% stiffness in global coordinatesys

Kelem=transpose(T)*K*T;

%Assembly of element siffness matrix

elementDOF=[2*node1-1,2*node1,2*node2-1,2*node2];

Ksys(elementDOF,elementDOF) = Ksys(elementDOF,elementDOF)+Kelem;

end

% sys local vector

Psys=zeros(TDOF,1);

psys(10,1)=-F;

%sys vector of nodal global displacement

dsys=zeros(TDOF,1);

% Define boundry condition

%applying cmrsing

for ielem=1:TDOF

if BCS(ielem,1)==1

Ksys(ielem,1:TDOF)=0;

Ksys(1:TDOF,ielem)=0;

Ksys(ielem,ielem)=1;

end

end

%global displacement vectors

dsys=Ksys\Psys;

%system force vector

Reac=zeros(TDOF,1);

% initial at the stress and force matrix

Stress=zeros(Nelem,1);

Force=zeros(Nelem,1);

for ielem=1:Nelem

node1 = Elcon(ielem,1);

node2 = Elcon(ielem,2);

elementDOF=[2*node1-1,2*node1,2*node2-1,2*node2];

uglob=dsys(elementDOF);

% dx=coord(node2,1)-coord(node1,1);

% dy=coord(node2,2)-coord(node1,2);

dx=coord(node2,1)-coord(node1,1);

dy=coord(node2,2)-coord(node1,2);

L=sqrt(dx^2+dy^2);

c=dx/L;

s=dy/L;

T1=[c,s;-s,c];

T=zeros(4);% ???

T(1:2,1:2)=T1;

T(3:4,3:4)=T1;

uloc= T*uglob;

%strain displacement monitor

B=[-1/L,0,1/L,0];

stress(ielem,1)=E*B*uglob;

Force(ielem,1)=A*stress(ielem,1)% ????

%local Element Force Vector

Floc=[-Force(ielem,1);0;Force(ielem,1);0]

%Global Element Force Vector

Fglob=transpose(T)*Floc

Reac(elementDOF)=Reac(elementDOF)+Fglob

end

Result :

Force =

0

0

0

0

0

0

0

0

0

Floc =

0

0

0

0

Fglob =

0

0

0

0

Reac =

0

0

0

0

0

0

0

0

0

0

0

0

Sometings goes wrong That I don't know where ? It should gives the result of forces

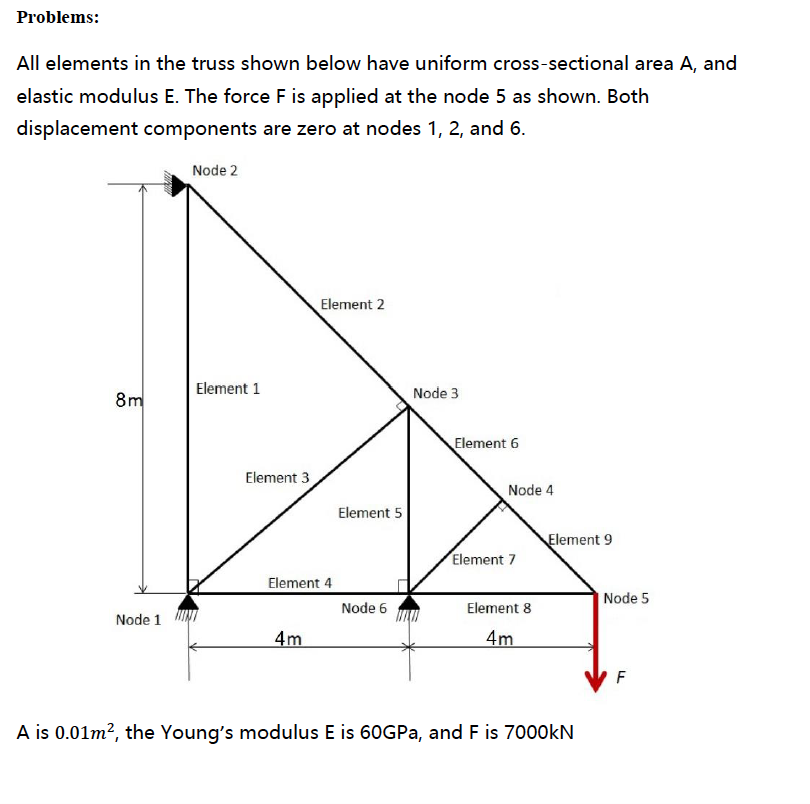
Problems: All elements in the truss shown below have uniform cross-sectional area A, and elastic modulus E. The force F is applied at the node 5 as shown. Both displacement components are zero at nodes 1, 2, and 6. Node 2 Element 2 Element 1 Node 3 Element 6 Element 3 Node 4 Element 5 ement 9 Element 7 Element 4 Node 5 Node 6 Element 8 Node 1 4 A is 0.01m2, the Young's modulus E is 60GPa, and F is 7000kN Problems: All elements in the truss shown below have uniform cross-sectional area A, and elastic modulus E. The force F is applied at the node 5 as shown. Both displacement components are zero at nodes 1, 2, and 6. Node 2 Element 2 Element 1 Node 3 Element 6 Element 3 Node 4 Element 5 ement 9 Element 7 Element 4 Node 5 Node 6 Element 8 Node 1 4 A is 0.01m2, the Young's modulus E is 60GPa, and F is 7000kN