Question: (1 point) Consider the differential equation dx = Ax(t) dt where A is a given matrix. Determine whether the equilibrium (0, 0) is a stable

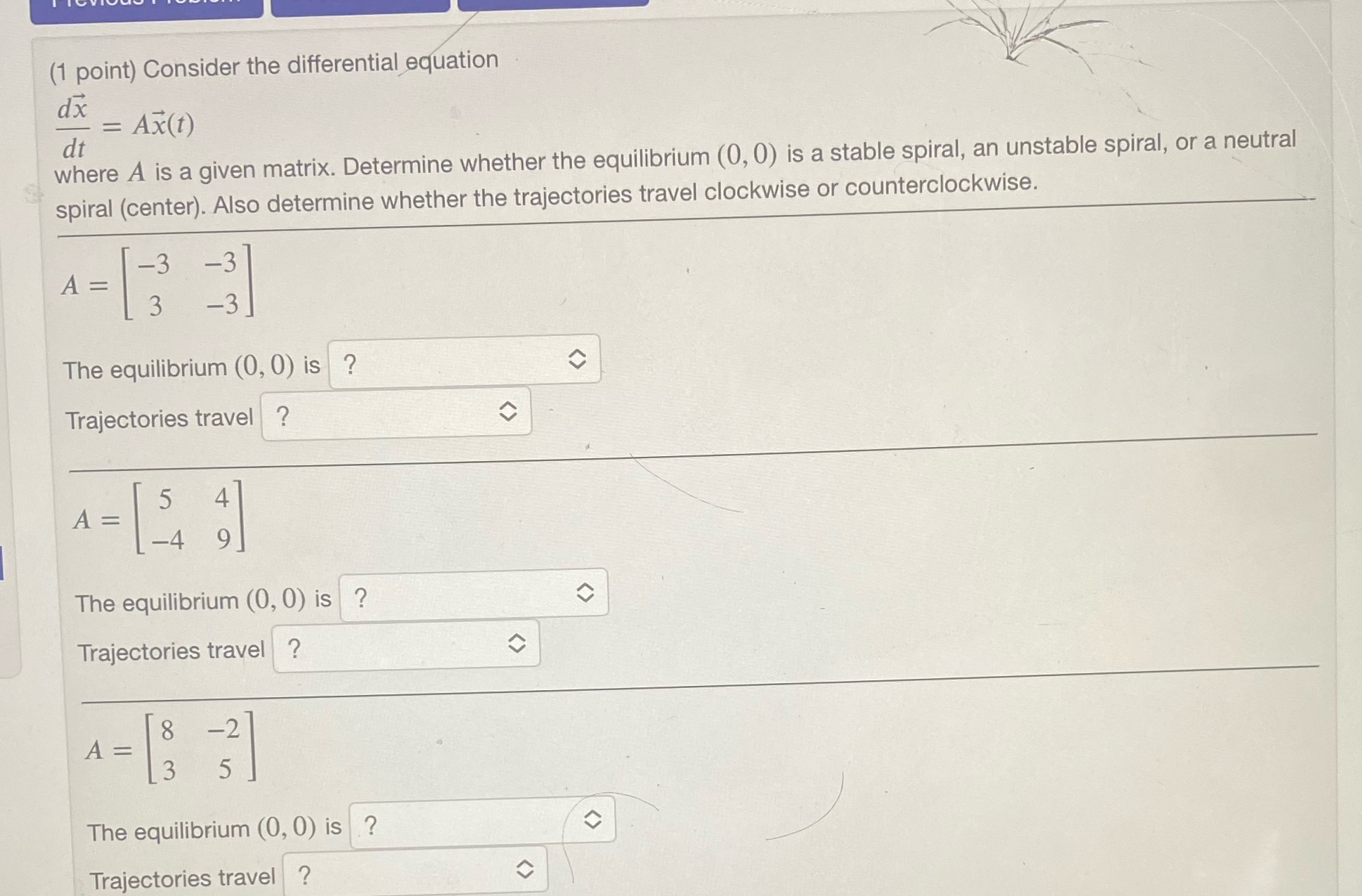
(1 point) Consider the differential equation dx = Ax(t) dt where A is a given matrix. Determine whether the equilibrium (0, 0) is a stable spiral, an unstable spiral, or a neutral spiral (center). Also determine whether the trajectories travel clockwise or counterclockwise. A = 3 The equilibrium (0, 0) is ? C Trajectories travel ? C A = 4 -4 9 The equilibrium (0, 0) is ? C Trajectories travel ? C A The equilibrium (0, 0) is ? C Trajectories travel ? C

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Integra Scienti | Dashbc | Course Switch 17C Section We X webwork.math.ucdavis.edu/webwork2/MAT17C-Temirgaliyeva-Fall-2023/Section_1... YouTube Maps Translate GE News my myucdavis Bookshelf:...

(1 point) Consider the differential equation dx = Ax(t) dt where A is a given matrix. Determine whether the equilibrium (0, 0) is a stable spiral, an unstable spiral, or a neutral spiral (center)....

(1 point) Consider the differential equation dx = Ax(t) dt where A is a given matrix. Determine whether the equilibrium (0, 0) is a stable node (sink), an unstable node (source), or a saddle point....

dy Consider the differential equation dt = 6y(y - 1) (y - 3). Use a phase-line analysis to determine whether each of the following equilibrium solutions are stable or unstable. The equilibrium...

1. Consider the differential equation y' = 13 - 3y' + 2y. (a) Find all equilibrium solutions and determine whether they are asymptotically stable or unstable. (Verify your answer.) (b) Sketch the...

dx Solve the equation f(x) = 0 to find the critical points of the given autonomous differential equation @ =f(x). Analyze the sign of f(x) to determine whether each critical point is stable or...

Exercise 1. Consider the differential equation & = f(x) for each given function f(x). In each case, (i) Find all equilibrium solutions of the differential equation in the specified interval. (ii)...

Hi, Can someone help me? #1 (1 point) Consider the slope field below for a differential equation. Use the graph to find the equilibrium solutions. TITITTT 11111 1111 1 Answer (separate by commas):y...

Name Student ID Final MAT 22B, Friday August 4, 2017 Instructions: This exam is closed notes, closed books, no calculators and no electronic devices of any kind. There are five problems worth 35...

What is the following prize worth today if money can earn 9% compounded monthly: $5000 payable two years from now, and a series of eleven $100 monthly payments beginning one month from now? A....

Where is the news media most influential? Why?

should change in net working capital be depreciated capiutal budgeting

Which one nike would use and explain why: raw material inventory, work in process (WIP) inventory, maintenance/ repair/operating (MRO) inventory and finished-goods inventory.

1. To learn how to develop a vision that can be communicated. To gain insight into the importance of game theory for communication strategies.

9. Take a view or attitude that you hold strongly. Search for information that is opposed to this view or attitude. Discuss.

2. In what way can we say that method affects the result we get?