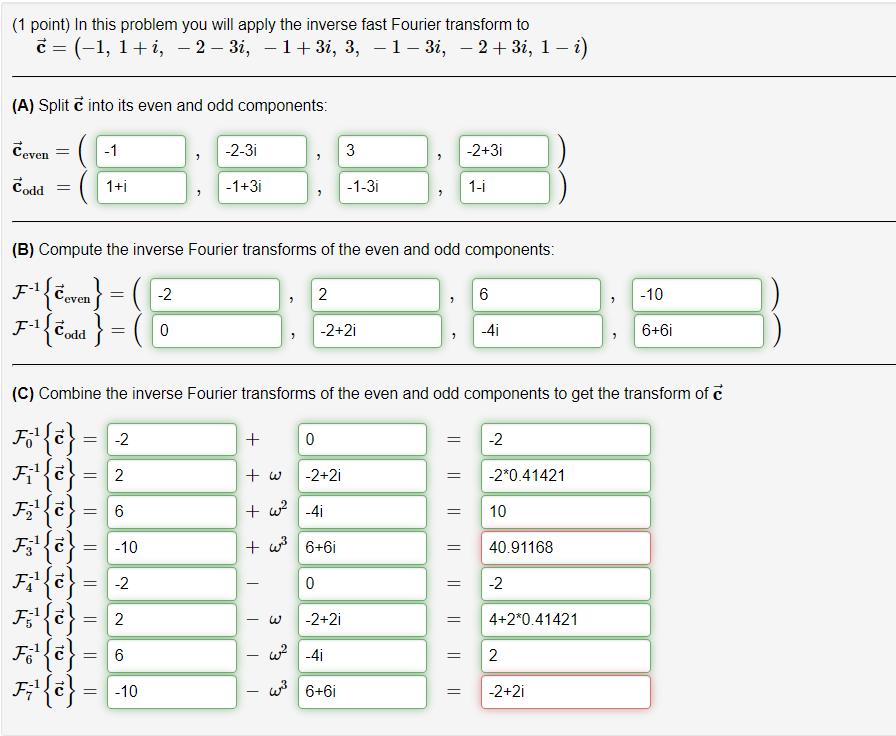
(1 point) In this problem you will apply the inverse fast Fourier transform to = (-1, 1+i, 2 3i, 1+3i, 3, 13i, 2+ 3i, 1 - i) - (A) Split into its even and odd components: Ceven -1 Codd = 1+i = = -2 = 2 9 = 2 -2-3i F{e} F {e} = 6 F{e} = -10 -1+3i (B) Compute the inverse Fourier transforms of the even and odd components: -2 F-{even} F- {Codd } = ( = 0 + 2 1 0 - 2 + w -2+2i +w -4i + 6+61 (C) Combine the inverse Fourier transforms of the even and odd components to get the transform of c Fo{e}= Fi{e}: = 6 F{e} = F3{e} = -10 F {e} = -2 F3{e} = 0 - w -2+2i -2+2i 3 -1-3i w4i 6i+6 | 1 = || -2+3i 1-i || = 6 -4i -2 = 10 -2*0.41421 40.91168 -2 4+2*0.41421 = 2 -10 6+6i = -2+2i