Question: 1. What shape (function) does the graph seem to follow? Does it agree with the expected theory for radioactive decay? 2. If you started

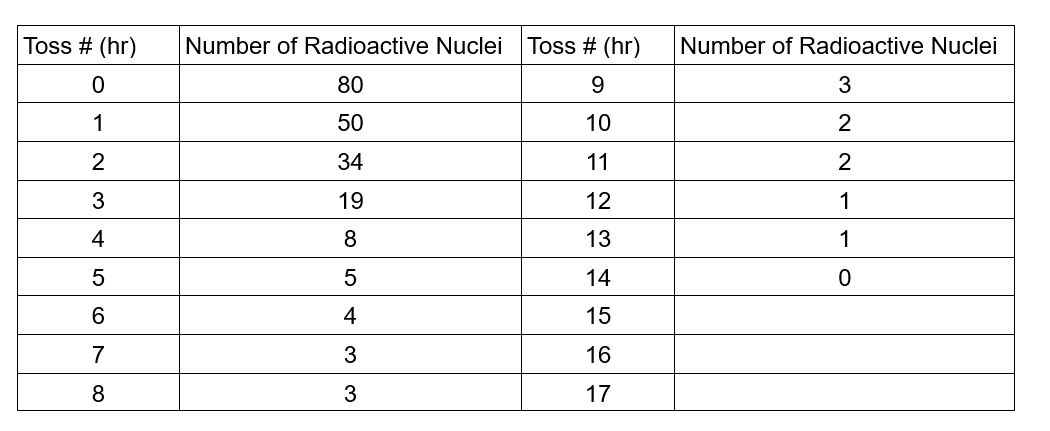
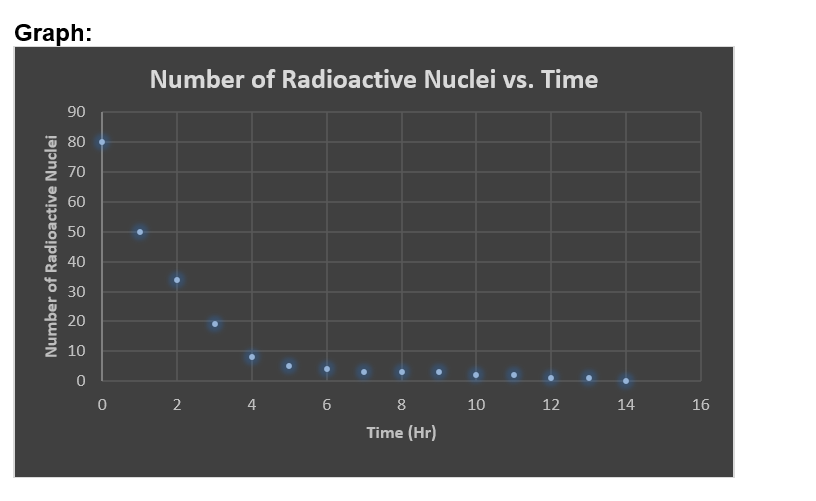
1. What shape (function) does the graph seem to follow? Does it agree with the expected theory for radioactive decay? 2. If you started with a sample of 600 radioactive nuclei, how many would remain undecayed after three half-lives? 3. How many half-lives would it take for 6.02 x 1023 nuclei to decay to 6.25% (0.376 x 1023) of the original number of nuclei? 4. Is there any way to predict when a specific piece of candy will land marked side up or "decayed?" If you could follow the fate of an individual atom in a sample of radioactive material, could you predict when it would decay? Explain. 5. Strontium-90 has a half-life of 28.8 years. If you start with a 10-gram sample of strontium-90, how much will be left after 115.2 years? Justify your answer. Toss # (hr) Number of Radioactive Nuclei Toss # (hr) Number of Radioactive Nuclei 0 80 9 3 1 50 10 2 2 34 11 2 3 19 12 1 4 8 13 1 5 5 14 0 6 4 15 7 8 33 16 17 Graph: Number of Radioactive Nuclei 90 80 70 60 50 40 30 20 10 0 Number of Radioactive Nuclei vs. Time 0 2 4 6 8 10 12 14 16 Time (Hr)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Physics Questions!

Munoz Manufacturing Company established the following standard price and cost data: Sales price $ 8.40 per unit Variable manufacturing cost $ 3.60 per unit Fixed manufacturing cost $ 2,000 total...

Is there any way to predict when a specific piece of candy will land marked side up, or "decayed"? If you could follow the fate of an individual atom in a sample of radioactive material, could you...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

Do you think that differences in reward practices across countries reflect differences in national cultures or other influences?

Consider the boarding stable feed problem presented in Chapter 3 as Problem 3-32 on page 112. Use Solver to create the Sensitivity Report for this LP problem. Use this report to answer the following...

Job costing, accounting for manufacturing overhead, budgeted rates. The Fasano Company uses a job-costing system at its Dover, Delaware, plant. The plant has a machining department and a finishing...

=+4. For the data in Exercise 1, suppose the historical standard deviation had been 0.1C instead of 0.2C. How would that change your answers to the questions in Exercise 3? Section 21.3

Jasper Company provided the following information for last year: Sales in units ............300,000 Selling price ................$9 Direct materials ...........$150,000 Direct labor...

What would the closing entries be for these adjustment entries? AJE # Account Name DR CR 1 wages expense 45,700 wages payable 45,700 payroll taxes 2,910 payroll taxes payable 2,910 2 unearned...

Bellevue Corporation reported the following selected information in its general ledger at December 31: All sales were on account. Some accounts receivable were collected. One account was written off;...

Question: Transfer function of a complex control system is given below. T(s): = 30s + 3s + s s6+3s5+4s + 6s + 5s +3s+2 a) Observe system's stability according to coefficient tests and mention your...

11. [10] The stochastic exponential of a constant, that is, the process & defined by Et = exp xp (aB - 1/2), t for some constant a, is a martingale. a. Prove the above statement directly, that is, by...

You sell t shirts at $10 each, and you have to pay the worker at each workstation $500/day.You went and hired a student who did some market research and told you that you could increase your price to...

1. The linkage shown below is made of two identical members with lengths of 0.8 m and masses of 3 kg. The left member is connected to the ground by a pin joint, and the right member is connected to...

What role would market research play in helping businesses improve their B 2 C communications ( and result in a higher frequency of positive C 2 B interactions ) ?

Suppose you owe $1,400 on your credit card. The annual percentage rate (APR) is 21%, compounded monthly. The credit card company says your minimum monthly payment is $28.28. a. If you make only this...

How is use of the word consistent helpful in fraud reports?

Does the length of term of pregnancy play a role in the level of education of the baby? Researchers in Norway followed over 1 million births between 1967 and 1988 and looked at the educational...

The following data represent the maximum wind speed (in knots) and atmospheric pressure (in millibars) for a random sample of hurricanes that originated in the Atlantic Ocean. Does atmospheric...

The median is different from 68. An analysis of the data reveals that there are 45 plus signs and 27 minus signs. Use the sign test to test the given alternative hypothesis at the = 0.05 level of...

Assessing Normality The accompanying histogram is constructed from the platelet counts of the 40 women included in Data Set 1 in the Appendix: Data Sets. If you plan to conduct further statistical...

Body Temperatures The normal quantile plot represents body temperatures of adults from Data Set 3 in the Appendix: Data Sets. z score 3 2.4 1.8 1.2 0.6 0 -0.6 -1.2 -1.8 -2.4 6.5 96.81 97.12 97.43...

Ages of Oscar-Winning Actresses The normal quantile plot represents the ages of actresses when they won Oscars. The data are from Data Set 11 in the Appendix: Data Sets. z score 3 2.4 1.8 1.2 0.6 0...