1- Write three Scheme procedures to simulate these three gates: AND, OR, and NOT, shown in the diagram in Figure 1. Test your procedures using all possible input combinations. Hint: Lecture slides showed the implementation of a not-gate in Scheme. (3 points)

2- Write a Scheme procedure to simulate the XOR gate, shown in the diagram in Figure 2. You must use AN

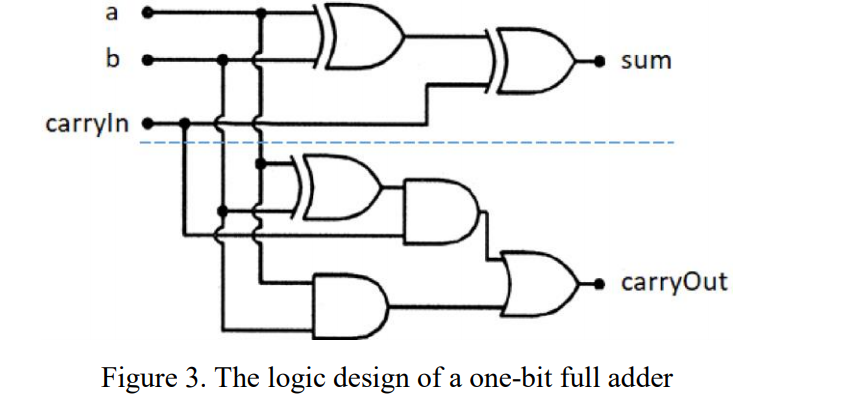
3- Define Scheme procedures to simulate the logic design given in the diagram in Figure 3. The procedures must follow the design in Figure and call the gate procedures that you defined in the previous questions and must return a pair with two elements '(c . s), where s is the binary sum of a, b, and x, while c is the carry-out. You will implement the procedure in three steps using three procedures, as listed below.

3.1 Write a procedure (halfAdder x a b) to generate (return) the sum bit s. The upper half of Fig. 3 (5 points)

3.2 Write a procedure (carry-out x a b) to generate (return) the carryOut bit c. The lower half of Fig. 3 (5 points)

3.3 Write a procedure (fullAdder x a b) to generate the pair output (c . s), where s is the output of the halfAdder procedure and c is the output of the carry-out procedure. The fullAdder is also called a one-bit adder.

CODE:

;Q1 (3 points)

; Put your code here:

(define OR-GATE (lambda (a b)

(define AND-GATE (lambda (a b)

(define NOT-GATE (lambda (a)

; Q2 (2 points)

; Put your code here:

(define XOR-GATE (lambda (a b)

; Test cases and expected output. Do not edit or remove.

(newline)

(Display "AND-Gate Output ")

(AND-GATE 0 0)

(AND-GATE 0 1)

(AND-GATE 1 0)

(AND-GATE 1 1)

;0

;0

;0

;1

(newline)

(Display "OR-Gate Output ")

(OR-GATE 0 0)

(OR-GATE 0 1)

(OR-GATE 1 0)

(OR-GATE 1 1)

;0

;1

;1

;1

(newline)

(newline)

(Display "XOR-Gate Output ")

(XOR-GATE 0 0)

(XOR-GATE 0 1)

(XOR-GATE 1 0)

(XOR-GATE 1 1)

;0

;1

;1

;0

;Q3.1 (5 points)

(define halfAdder (lambda (x a b)

;Q3.2 (5 points)

(define carry-out (lambda (x a b)

;Q3.3 (5 points)

(define fullAdder (lambda (x a b)

; Test cases and expected output. Do not edit or remove.

(newline)

(Display "halfAdder Output ")

(halfAdder 0 0 0)

(halfAdder 0 0 1)

(halfAdder 0 1 0)

(halfAdder 0 1 1)

(halfAdder 1 0 0)

(halfAdder 1 0 1)

(halfAdder 1 1 0)

(halfAdder 1 1 1)

;halfAdder Output

;0

;1

;1

;0

;1

;0

;0

;1

(newline)

(Display "fullAdder Output ")

(fullAdder 0 0 0)

(fullAdder 0 0 1)

(fullAdder 0 1 0)

(fullAdder 0 1 1)

(fullAdder 1 0 0)

(fullAdder 1 0 1)

(fullAdder 1 1 0)

(fullAdder 1 1 1)

;(0 . 0)

;(0 . 1)

;(0 . 1)

;(1 . 0)

;(0 . 1)

;(1 . 0)

;(1 . 0)

;(1 . 1)

;Q4.1 (4 points)

(define tail (lambda (lst)

;Q4.2 (4 points)

(define rmtail (lambda (lst)

;Q4.3 (4 points)

; Write the answers in comments

;1) What is the size-n problem of your procedure?

;2) What are the stopping condition and its return value?

;3) What is the size-(n-1) problem?

;4) What are the steps to construct the size-n problem solution from the size-(n-1) solution?

;Q4.4 (18 points)

(define n-bit-adder (lambda (L1 L2 n)

; Test cases. Do not edit or remove.

(define X1 '(0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0) )

(define X2 '(1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1) )

(define X3 '(0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1) )

(define X4 '(1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0) )

(define X5 '(1 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1) )

(define X6 '(1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 0) )

(Display "n-bit-adder Output ")

(newline)

(Display "n-bit-adder Output ")

(n-bit-adder1 X1 X2 32)

(n-bit-adder1 X3 X4 32)

(n-bit-adder1 X5 X6 32)

(n-bit-adder1 X2 X3 32)

(n-bit-adder1 X4 X5 32)

(n-bit-adder1 X1 X6 32)

;(0 (1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1))

;(0 (1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1))

;(1 (1 0 1 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 1))

;(1 (0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0))

;(1 (1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1))

;(0 (1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 0))

sum carryln carryOut Migur 31 he, log c (les gn ofn onc bit full acl(let, sum carryln carryOut Migur 31 he, log c (les gn ofn onc bit full acl(let