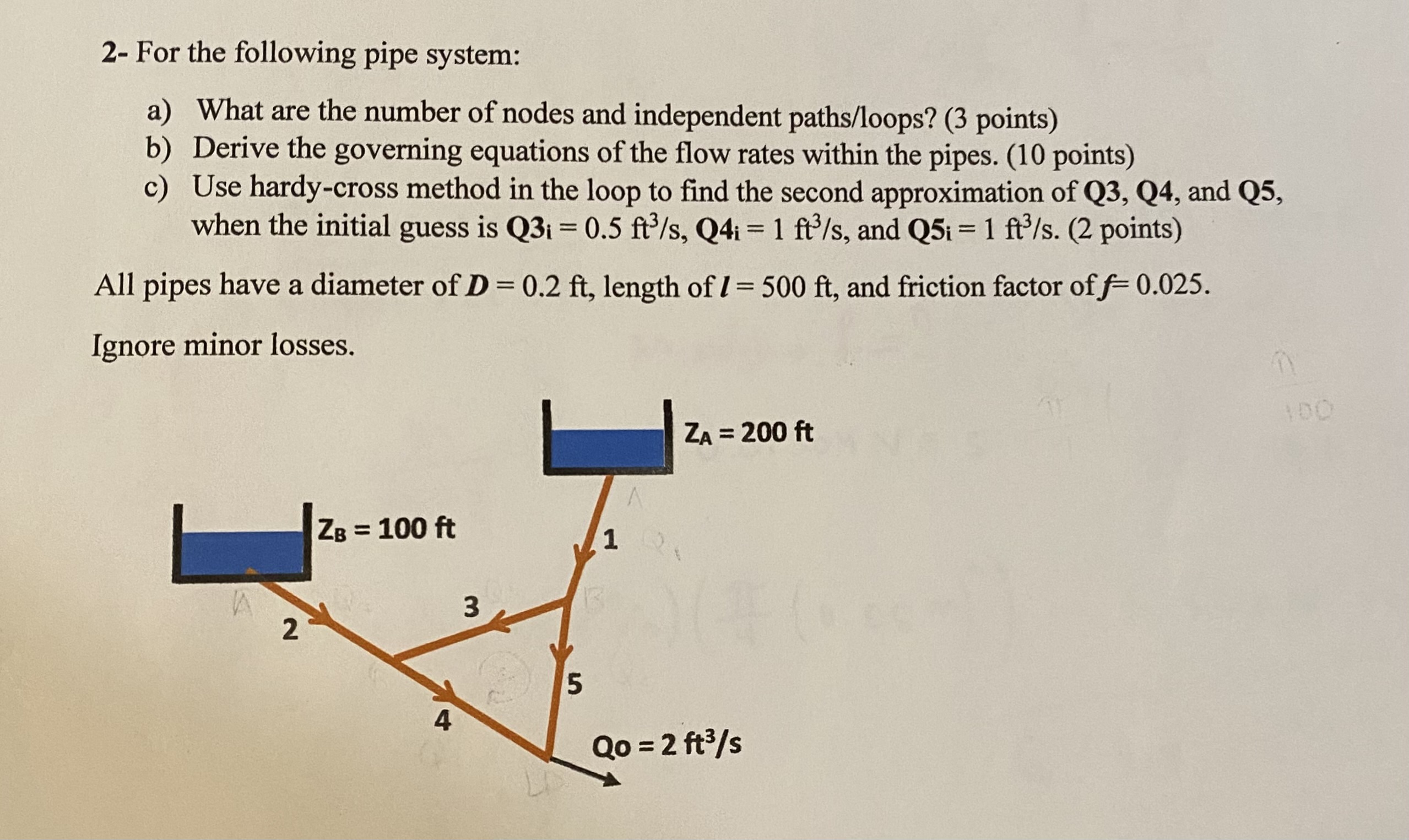
2- For the following pipe system: a) What are the number of nodes and independent paths/loops? (3 points) b) Derive the governing equations of the flow rates within the pipes. (10 points) c) Use hardy-cross method in the loop to find the second approximation of Q3, Q4, and Q5, when the initial guess is Q3 = 0.5 ft/s, Q4i = 1 ft/s, and Q5i = 1 ft/s. (2 points) All pipes have a diameter of D = 0.2 ft, length of 1 = 500 ft, and friction factor of f= 0.025. Ignore minor losses. I ZB = 100 ft 3 A 1 ZA = 200 ft 2 4 5 Qo = 2 ft/s 100