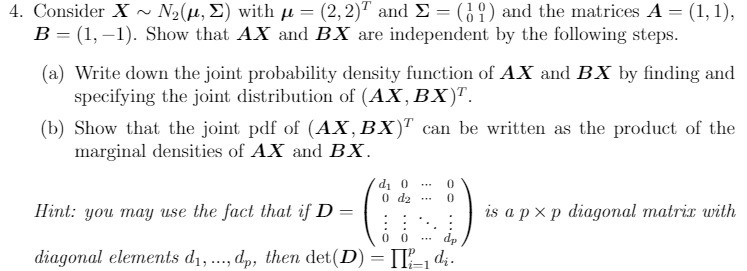
4. Consider X ~ N2(u, E) with A = (2,2)' and E = ( ) and the matrices A = (1, 1), B = (1, -1). Show that AX and BX are independent by the following steps. (a) Write down the joint probability density function of AX and BX by finding and specifying the joint distribution of (AX, BX) T. (b) Show that the joint pdf of (AX, BX)" can be written as the product of the marginal densities of AX and BX. d1 0 0 d2 0 Hint: you may use the fact that if D = is a p x p diagonal matrix with diagonal elements di, ..., dp, then det( D) = DIP