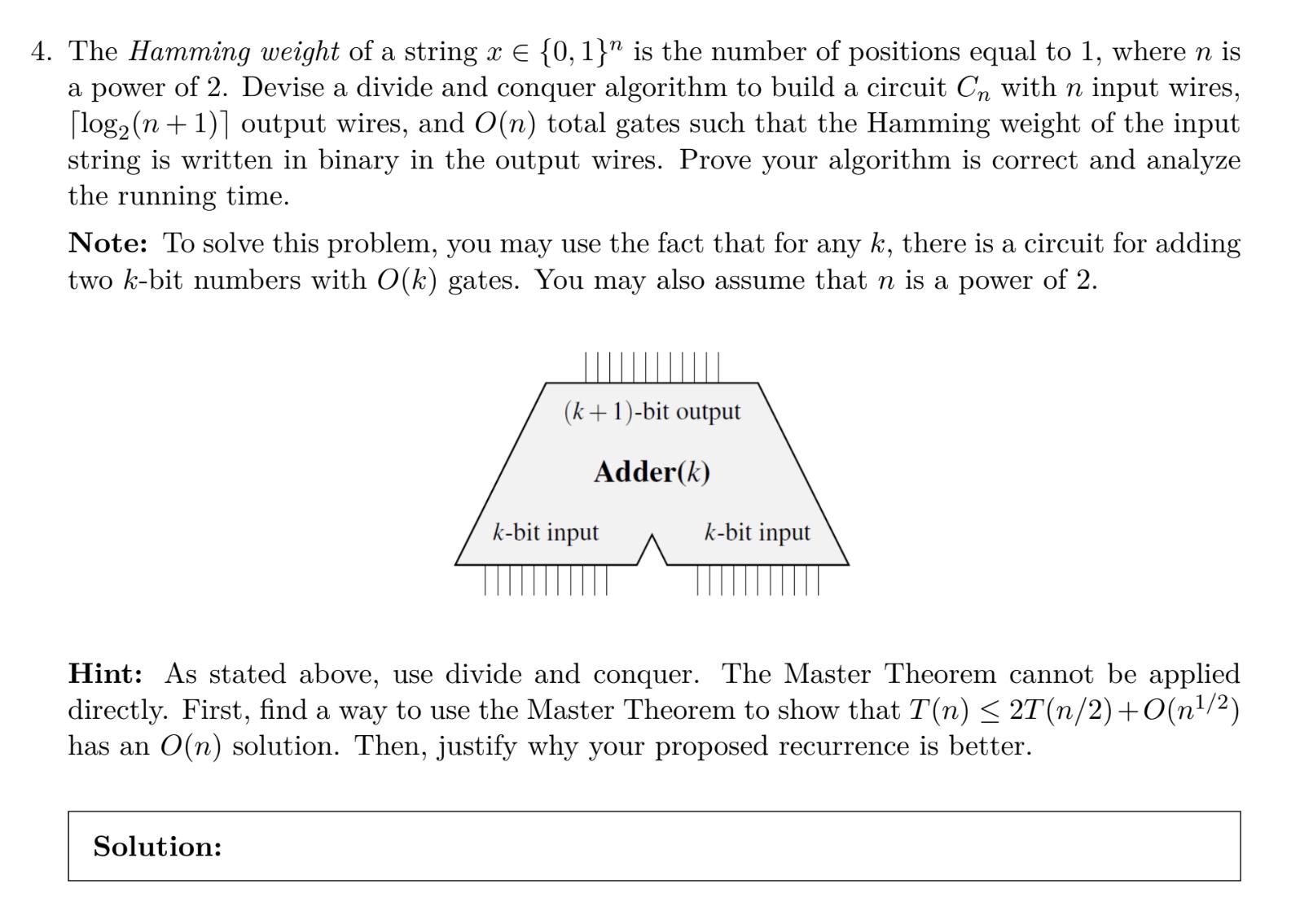
4. The Hamming weight of a string x = {0, 1}" is the number of positions equal to 1, where n is a power of 2. Devise a divide and conquer algorithm to build a circuit Cn with n input wires, [log (n+1)] output wires, and O(n) total gates such that the Hamming weight of the input. string is written in binary in the output wires. Prove your algorithm is correct and analyze the running time. Note: To solve this problem, you may use the fact that for any k, there is a circuit for adding two k-bit numbers with O(k) gates. You may also assume that n is a power of 2. (k+1)-bit output Adder(k) Solution: k-bit input k-bit input Hint: As stated above, use divide and conquer. The Master Theorem cannot be applied directly. First, find a way to se the Master Theorem to show that T(n) 2T(n/2) +O(n/) has an O(n) solution. Then, justify why your proposed recurrence is better.