Question: 5. Define h(x) = x' sin , for x # 0 and h(0) = 0. Show that h is differentiable everywhere and that h' is

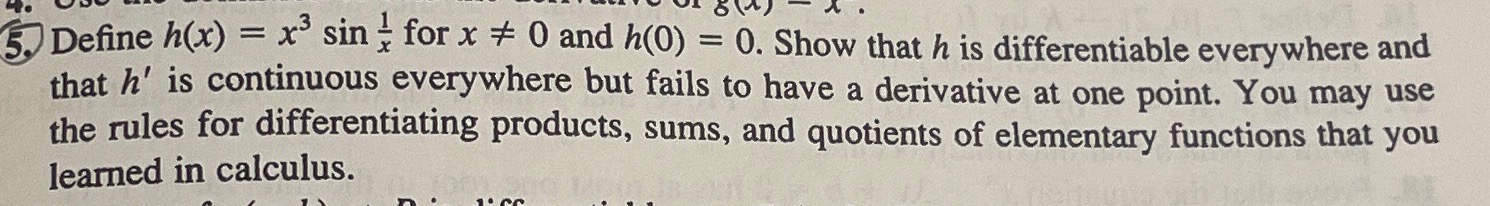
5. Define h(x) = x' sin , for x # 0 and h(0) = 0. Show that h is differentiable everywhere and that h' is continuous everywhere but fails to have a derivative at one point. You may use the rules for differentiating products, sums, and quotients of elementary functions that you learned in calculus

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

19 24 Explain using Theorems 4 5 6 and 8 why the fun tion is continuous at every number in its domain State the domain no 19 F x 4 THEOREM If f and g are continuous at a and c is a constant then the...

41. lim x - 1 42. lim 1- Vx 1 1 1-x 71. f(x) = x2 +1, ifx so 1-x, ifx > 0 43. lim *+x2-273 x - x2 44. lim x+x2- 2x3 x - x2 72. f(x) = 3x + 2, ifx 1 57. lim sin x 58. lim cotx x+ 1, ifx 3 NI 60. lim -...

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

MATH 140 EXAM 1 Professor: Dr. J. Beyers NAME________________________ INSTRUCTIONS The exam is worth 100 points. There are 20 problems (each worth 5 points). This quiz is open book and open notes,...

Problem 3.20. Note that while the second part of this problem can be solved using the first part, but there are other ways to solve Part 2. (a) Suppose 9 R R and that g(x* + h) limh0 (h) = 0. =...

11. [-/6 Points] DETAILS Consider this function y = f(x) on the domain (-co, co). f ( x ) = x2 sin( >)+ 16 ifx # 0 16 if x = 0 (a) If x+ 0 , f '(x)= 2x sin x - 5 cos n X (b) Answer these multiple...

2.2.44 please explain how to get the solution step by step. 44. The function f(x) defined as f (x ) = x2 . sin(-) if x * 0 0 if x = 0 (shown at the top of the next page) is continuous at 0 because we...

(3) Define sinc x = sin x for x * 0 and sinc 0 = 1. (a Show that lim sinc x = 1. x-+0 (b) Show that lim sinc x = lim sinc x = 0. (c) Show that sinc x = 0 if and only if x is a nonzero integer...

Is the function defined by 2x 3 if x 2 2x 3 if x 2 6 f x x 8 f x x 0 continuous at x 0 At x 1 At x 2 Find all points of discontinuity off where fis defined 10 f x if x 0 if x 0 NO x 1 if x 1 x 1 if x...

the figure above shows the graph of the differentiable function g and the line tangent to the graph of g at the point(5,2). let f be the function given by f(x)= integral from 0 to x g(t)dt. let h be...

Particle deposition rate J on a wafer that is parallel to airflow is given by J= nu, where n is the particle density and u is the sum of gravitational and diffusive settling velocities, - 5 x 10-cm/s...

On 1 July 2019. Galaxy Bhd acquired Pluto Bhd through an acquisition of 80% of the ordinary shares. Pluto had in issue 200,000 ordinary shares of RM1 each. On the same date, Galaxy Bhd acquired...

Which of these statements best fits how a behavioral economist might view a situation? If you lost $ 2 0 today but then found $ 2 0 later on , you feel neutral because ir's as if you never lost...

A company is preparing completing their Cash Budget. The following data has been prepared for cash receipts and payments. January February March Cash receipts $1,061,200 $1,182,400 $1,091,700 Cash...