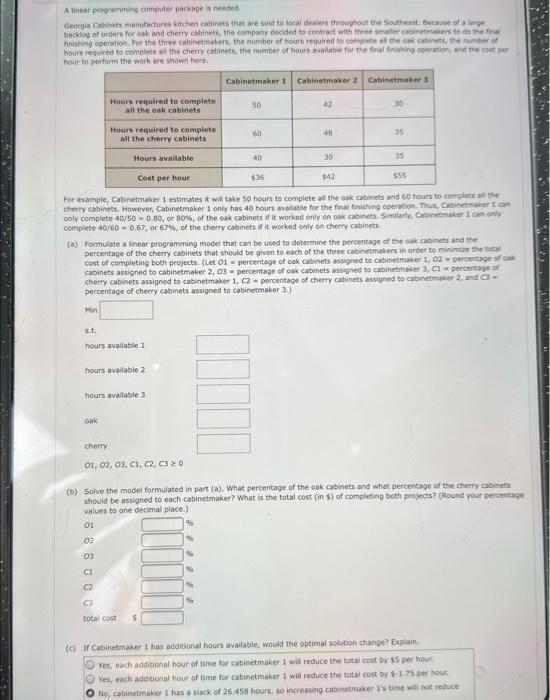
Question: A linear programning computhe packinge is netded. backlog of orders foe oak and cherty cabinets, the company decided to conkract nitti three smanter cabiretmakers to
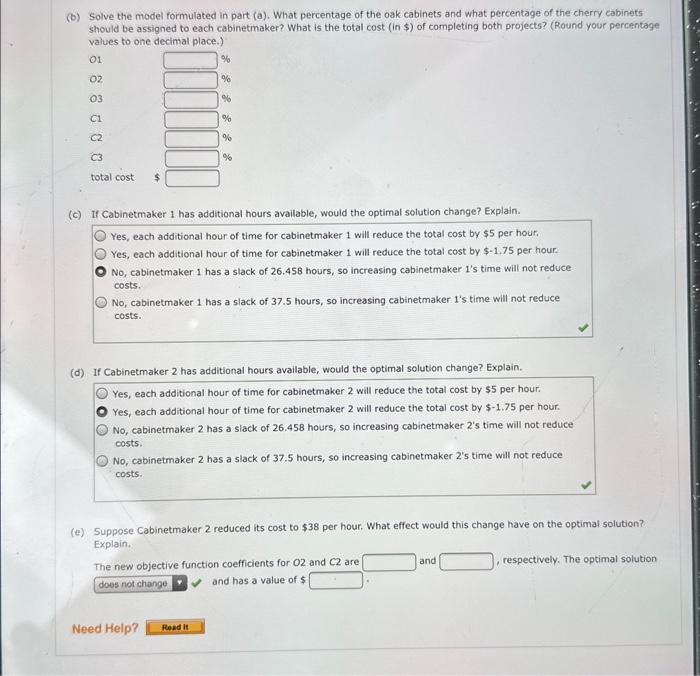
A linear programning computhe packinge is netded. backlog of orders foe oak and cherty cabinets, the company decided to conkract nitti three smanter cabiretmakers to da the find hour to perform the werk are shown herie. For example. Cabinetmaker 1 estimates it will take 50 hours to complete all the oak cabinets and 60 trours to complete alt the chery cabinets. Hewever, Cabinetmaker 1 only has 40 hours avalable for the find firithing operation, Tous, Cabinetimyeer 1 can only complete 40/50=0.80, or 80%, of the oak cabinets if it worked only oa oak cabinets. 5 inilarty. Cabinetimaker 1 can crily complete 40/60=0.67, or 67%, of the cherty cabinets it it worked only on chemy cabinett. (a) Formulate a Linear programming model that can be used to determine the percentage of the oakcabinets and the percentage of the cherry cabinets that should be given to ebch of the theee cabinetmakers in order to minimize the tacal cost of completing both projects. (Let O1 = percevtege of osk cabinets assigned to cabinetriaker 1, on = percentage df cak cabinets assigned to cabinetmaker 2,03 = percentaje of cak cabinets assigned to cabinetriaker 3, of = percermase of cherry cabinets assigned to cabinebmaket 1,q= percentage of cherry cabinets assigned to cabinetmakee 2 , and C3= percentage of cherry cabinets assigned to cabinetmaker 3.) (b) Solve the model formulated in part (a). What percentage of the oak cabinets and what percentage of the cherrr cabinats should be assigned to each cabinetmaker? What is the total cost (in $ ) of completing both projects? (Round your perceetage values to one cecimal place.) O1 02 03 C1 C2 C3 total cost (c). If Cabinetmaker 1 has addibional hours available, would the optimal solvtion chache? Explair. Yes, each additional hodr of time for cabinetrraker 1 will reduce the total cost by \$\$s per houc. Yes, esch add tional hour of time for cabinetmaker 1 will reduce the total cost Dy $1.75 per hour. No, cabinetmaker 1 has a stack of 26.45 t houre, wo increasing cabinetmaker 1 ts time will not ieduce (b) Solve the model formulated in part (a). What percentage of the oak cabinets and what percentage of the cherry cabinets should be assigned to each cabinetmaker? What is the total cost (in \$) of completing both projects? (Round your percentage values to one decimal place.) \begin{tabular}{l|l} O1 & % \\ O2 & % \\ O3 & % \\ C1 & % \\ C2 & % \\ C3 & % \\ total cost & $ \end{tabular} (c) If Cabinetmaker 1 has additional hours available, would the optimal solution change? Explain. Yes, each additional hour of time for cabinetmaker 1 will reduce the total cost by $5 per hour. Yes, each additional hour of time for cabinetmaker 1 will reduce the total cost by $1.75 per hour. No, cabinetmaker 1 has a slack of 26.458 hours, so increasing cabinetmaker 1 's time will not reduce costs. No, cabinetmaker 1 has a slack of 37.5 hours, so increasing cabinetmaker 1 's time will not reduce costs. (d) If Cabinetmaker 2 has additional hours available, would the optimal solution change? Explain. Yes, each additional hour of time for cabinetmaker 2 will reduce the total cost by $5 per hour: Yes, each additional hour of time for cabinetmaker 2 will reduce the total cost by $1.75 per hour. No, cabinetmaker 2 has a slack of 26.458 hours, so increasing cabinetmaker 2 's time will not reduce costs. No, cabinetmaker 2 has a slack of 37.5 hours, so increasing cabinetmaker 2 's time will not reduce costs. (e) Suppose Cabinetmaker 2 reduced its cost to $38 per hour. What effect would this change have on the optimal solution? Explain. The new objective function coefficients for O2 and C2 are , respectively. The optimal solution and has a value of $