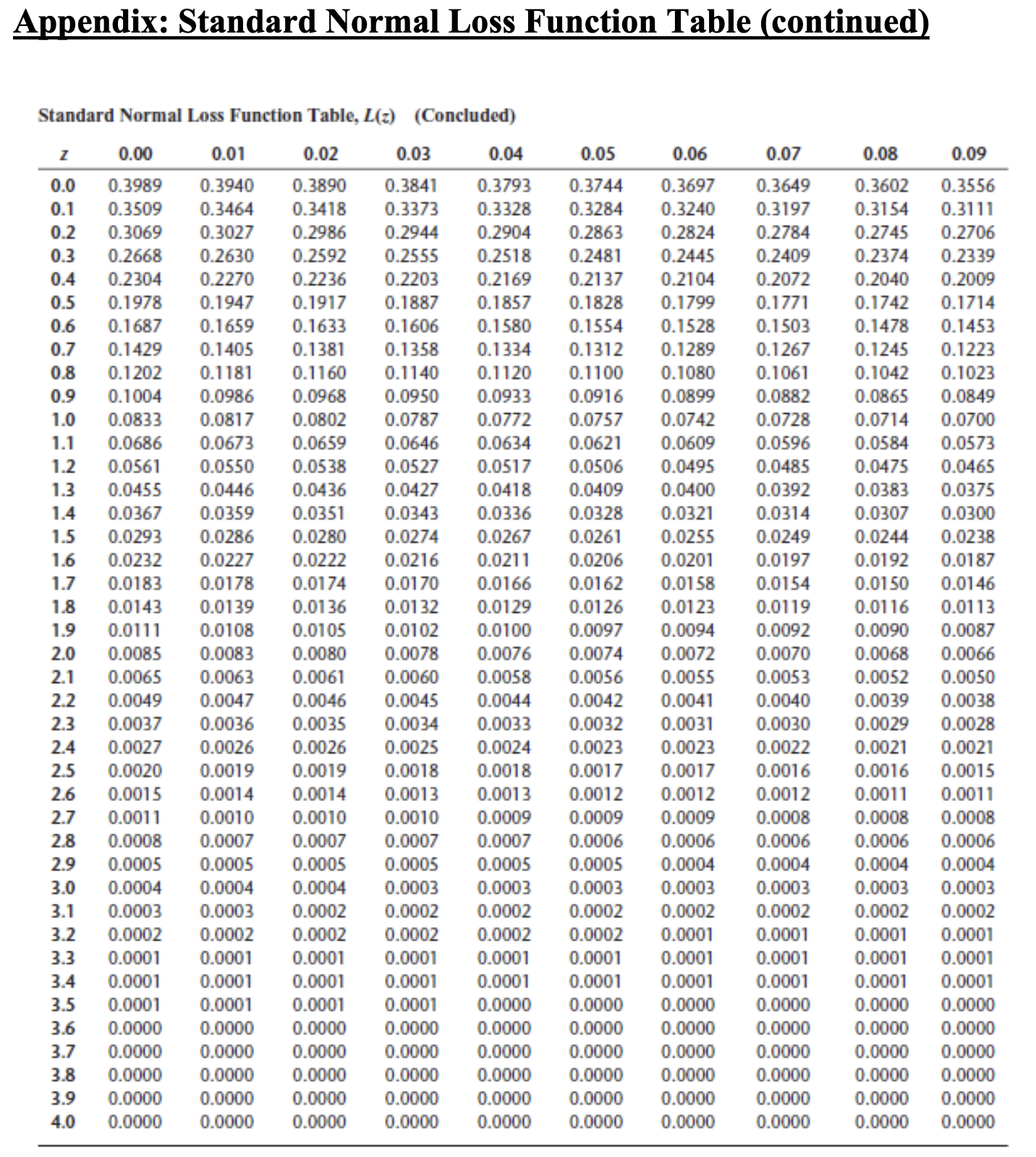
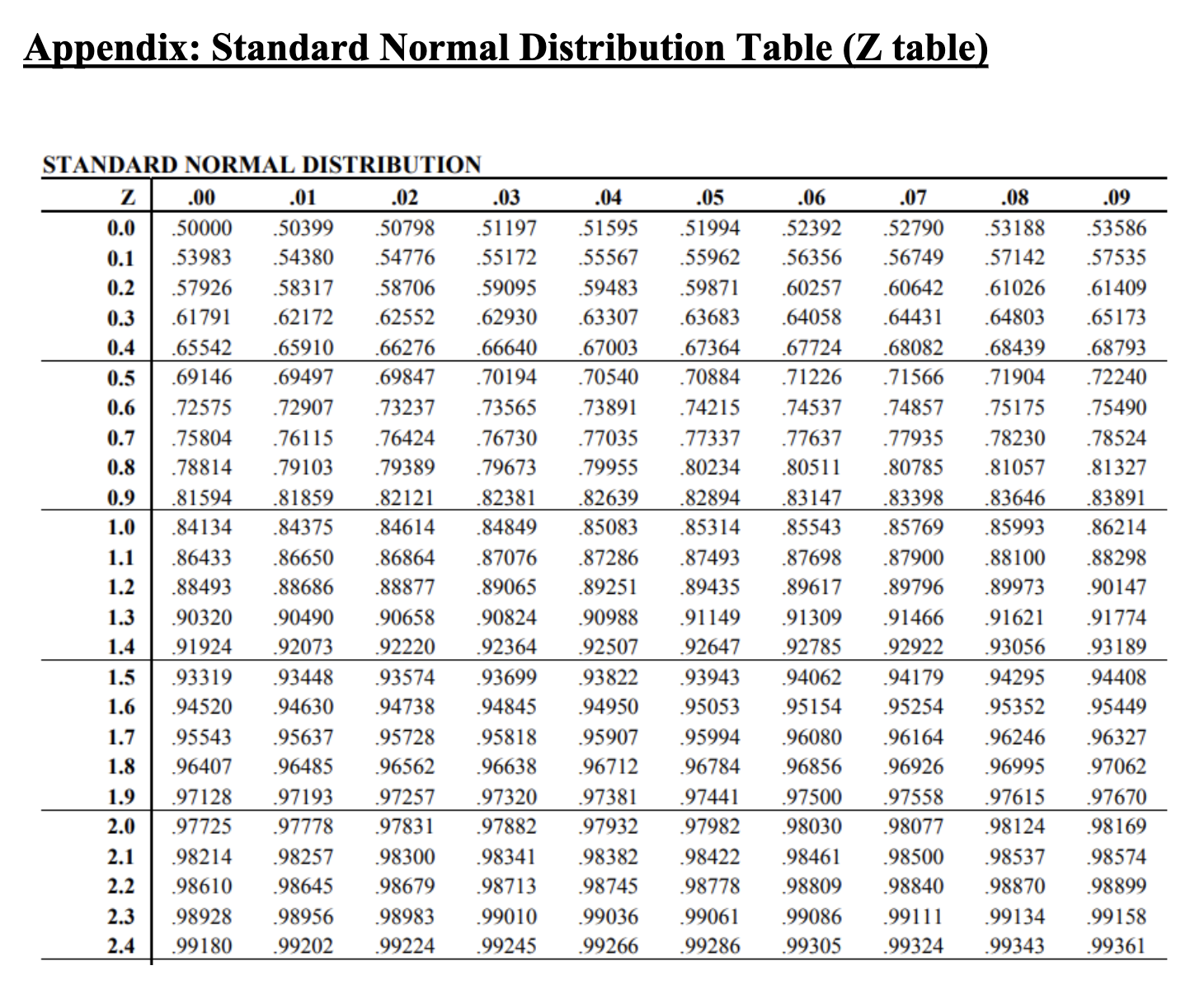
Appendix: Standard Normal Loss Function Table Appendix: Standard Normal Distribution Table ( Z table) Question 5 (Risk Pooling Strategies). [8 points] An apparel company is selling a newly designed dress to its customers located in two different regions. It is estimated that the customer demands from both regions follow a normal distribution with mean 1,000 and standard deviation 200. Based on historical sales information, the tastes of the customers from these two regions towards fashion apparel are very different, and it is assumed that correlation coefficient of the demands from the two regions is equal to -1 (i.e., their demands are perfectly negatively correlated). The company runs a centralized warehouse, where all inventory is held at the warehouse and will be shipped to the two regions to fulfill the customer orders. Based on the above demand forecast, what is the optimal inventory that the company should order for the warehouse? Appendix: Standard Normal Loss Function Table (continued) Standard Normal Loss Function Table, L(z) (Concluded) \begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|} \hlinez & 0.00 & 0.01 & 0.02 & 0.03 & 0.04 & 0.05 & 0.06 & 0.07 & 0.08 & 0.09 \\ \hline 0.0 & 0.3989 & 0.3940 & 0.3890 & 0.3841 & 0.3793 & 0.3744 & 0.3697 & 0.3649 & 0.3602 & 0.3556 \\ \hline 0.1 & 0.3509 & 0.3464 & 0.3418 & 0.3373 & 0.3328 & 0.3284 & 0.3240 & 0.3197 & 0.3154 & 0.3111 \\ \hline 0.2 & 0.3069 & 0.3027 & 0.2986 & 0.2944 & 0.2904 & 0.2863 & 0.2824 & 0.2784 & 0.2745 & 0.2706 \\ \hline 0.3 & 0.2668 & 0.2630 & 0.2592 & 0.2555 & 0.2518 & 0.2481 & 0.2445 & 0.2409 & 0.2374 & 0.2339 \\ \hline 0.4 & 0.2304 & 0.2270 & 0.2236 & 0.2203 & 0.2169 & 0.2137 & 0.2104 & 0.2072 & 0.2040 & 0.2009 \\ \hline 0.5 & 0.1978 & 0.1947 & 0.1917 & 0.1887 & 0.1857 & 0.1828 & 0.1799 & 0.1771 & 0.1742 & 0.1714 \\ \hline 0.6 & 0.1687 & 0.1659 & 0.1633 & 0.1606 & 0.1580 & 0.1554 & 0.1528 & 0.1503 & 0.1478 & 0.1453 \\ \hline 0.7 & 0.1429 & 0.1405 & 0.1381 & 0.1358 & 0.1334 & 0.1312 & 0.1289 & 0.1267 & 0.1245 & 0.1223 \\ \hline 0.8 & 0.1202 & 0.1181 & 0.1160 & 0.1140 & 0.1120 & 0.1100 & 0.1080 & 0.1061 & 0.1042 & 0.1023 \\ \hline 0.9 & 0.1004 & 0.0986 & 0.0968 & 0.0950 & 0.0933 & 0.0916 & 0.0899 & 0.0882 & 0.0865 & 0.0849 \\ \hline 1.0 & 0.0833 & 0.0817 & 0.0802 & 0.0787 & 0.0772 & 0.0757 & 0.0742 & 0.0728 & 0.0714 & 0.0700 \\ \hline 1.1 & 0.0686 & 0.0673 & 0.0659 & 0.0646 & 0.0634 & 0.0621 & 0.0609 & 0.0596 & 0.0584 & 0.0573 \\ \hline 1.2 & 0.0561 & 0.0550 & 0.0538 & 0.0527 & 0.0517 & 0.0506 & 0.0495 & 0.0485 & 0.0475 & 0.0465 \\ \hline 1.3 & 0.0455 & 0.0446 & 0.0436 & 0.0427 & 0.0418 & 0.0409 & 0.0400 & 0.0392 & 0.0383 & 0.0375 \\ \hline 1.4 & 0.0367 & 0.0359 & 0.0351 & 0.0343 & 0.0336 & 0.0328 & 0.0321 & 0.0314 & 0.0307 & 0.0300 \\ \hline 1.5 & 0.0293 & 0.0286 & 0.0280 & 0.0274 & 0.0267 & 0.0261 & 0.0255 & 0.0249 & 0.0244 & 0.0238 \\ \hline 1.6 & 0.0232 & 0.0227 & 0.0222 & 0.0216 & 0.0211 & 0.0206 & 0.0201 & 0.0197 & 0.0192 & 0.0187 \\ \hline 1.7 & 0.0183 & 0.0178 & 0.0174 & 0.0170 & 0.0166 & 0.0162 & 0.0158 & 0.0154 & 0.0150 & 0.0146 \\ \hline 1.8 & 0.0143 & 0.0139 & 0.0136 & 0.0132 & 0.0129 & 0.0126 & 0.0123 & 0.0119 & 0.0116 & 0.0113 \\ \hline 1.9 & 0.0111 & 0.0108 & 0.0105 & 0.0102 & 0.0100 & 0.0097 & 0.0094 & 0.0092 & 0.0090 & 0.0087 \\ \hline 2.0 & 0.0085 & 0.0083 & 0.0080 & 0.0078 & 0.0076 & 0.0074 & 0.0072 & 0.0070 & 0.0068 & 0.0066 \\ \hline 2.1 & 0.0065 & 0.0063 & 0.0061 & 0.0060 & 0.0058 & 0.0056 & 0.0055 & 0.0053 & 0.0052 & 0.0050 \\ \hline 2.2 & 0.0049 & 0.0047 & 0.0046 & 0.0045 & 0.0044 & 0.0042 & 0.0041 & 0.0040 & 0.0039 & 0.0038 \\ \hline 2.3 & 0.0037 & 0.0036 & 0.0035 & 0.0034 & 0.0033 & 0.0032 & 0.0031 & 0.0030 & 0.0029 & 0.0028 \\ \hline 2.4 & 0.0027 & 0.0026 & 0.0026 & 0.0025 & 0.0024 & 0.0023 & 0.0023 & 0.0022 & 0.0021 & 0.0021 \\ \hline 2.5 & 0.0020 & 0.0019 & 0.0019 & 0.0018 & 0.0018 & 0.0017 & 0.0017 & 0.0016 & 0.0016 & 0.0015 \\ \hline 2.6 & 0.0015 & 0.0014 & 0.0014 & 0.0013 & 0.0013 & 0.0012 & 0.0012 & 0.0012 & 0.0011 & 0.0011 \\ \hline 2.7 & 0.0011 & 0.0010 & 0.0010 & 0.0010 & 0.0009 & 0.0009 & 0.0009 & 0.0008 & 0.0008 & 0.0008 \\ \hline 2.8 & 0.0008 & 0.0007 & 0.0007 & 0.0007 & 0.0007 & 0.0006 & 0.0006 & 0.0006 & 0.0006 & 0.0006 \\ \hline 2.9 & 0.0005 & 0.0005 & 0.0005 & 0.0005 & 0.0005 & 0.0005 & 0.0004 & 0.0004 & 0.0004 & 0.0004 \\ \hline 3.0 & 0.0004 & 0.0004 & 0.0004 & 0.0003 & 0.0003 & 0.0003 & 0.0003 & 0.0003 & 0.0003 & 0.0003 \\ \hline 3.1 & 0.0003 & 0.0003 & 0.0002 & 0.0002 & 0.0002 & 0.0002 & 0.0002 & 0.0002 & 0.0002 & 0.0002 \\ \hline 3.2 & 0.0002 & 0.0002 & 0.0002 & 0.0002 & 0.0002 & 0.0002 & 0.0001 & 0.0001 & 0.0001 & 0.0001 \\ \hline 3.3 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 \\ \hline 3.4 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0001 \\ \hline 3.5 & 0.0001 & 0.0001 & 0.0001 & 0.0001 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 \\ \hline 3.6 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 \\ \hline 3.7 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 \\ \hline 3.8 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 \\ \hline 3.9 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 \\ \hline 4.0 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 & 0.0000 \\ \hline \end{tabular}