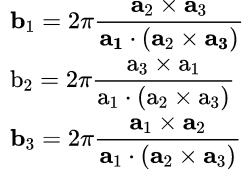
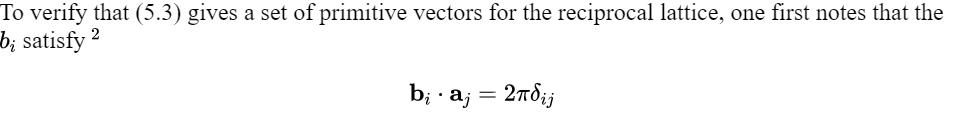
(b) Suppose primitive vectors are constructed from the b; in the same manner (Eq. (5.3)) as the bi are constructed from the a, Prove that these vectors are just the a themselves; i.e., show that b2 x b3 27 b (b2 x b3) = a1, etc. (Hint: Write b, in the numerator (but not b2 ) in terms of the a;, use the vector identity Ax (Bx C) = B(A C) (A B), and appeal to the orthogonality relations (5.4) and the result (5.15) above ) X b = 27 a1 : (z X ) b2 = 27- aj ( X ) 2 b3 = 27- aj ( X ) b; satisfy 2 b; aj = 27dij