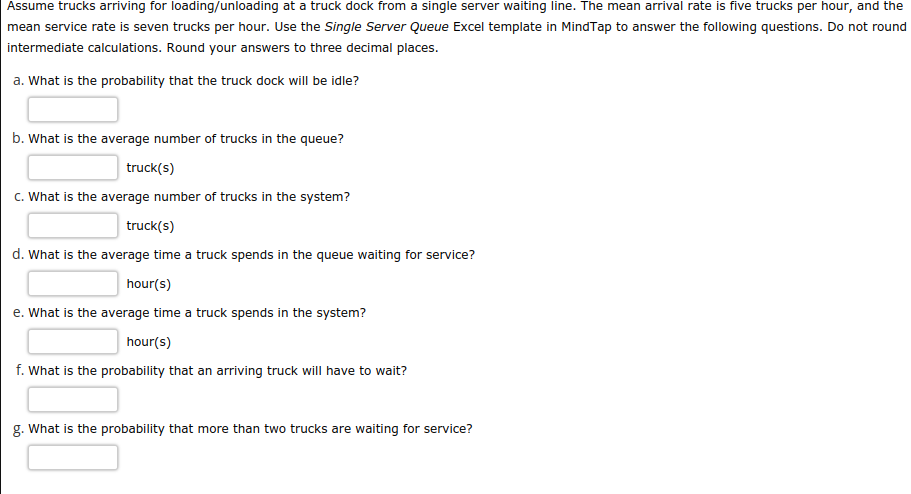
\begin{tabular}{|c|c|} \hline Lambda & 10 \\ \hline Mu & 12 \\ \hline Probability system is empty & 0.167 \\ \hline Average number waiting for service in the queue & 4.167 \\ \hline Average number in system (queue and in service) & 5.000 \\ \hline Average time waiting for service (time in queue) & 0.417 \\ \hline vaiting time in system (waiting time plus service time) & 0.500 \\ \hline Probability arrival has to wait & 0.833 \\ \hline n= & 3 \\ \hline bability of n units in the system & 0.096 \\ \hline \end{tabular} Assume trucks arriving for loading/unloading at a truck dock from a single server waiting line. The mean arrival rate is five trucks per hour, and the mean service rate is seven trucks per hour. Use the Single Server Queue Excel template in MindTap to answer the following questions. Do not round intermediate calculations. Round your answers to three decimal places. a. What is the probability that the truck dock will be idle? b. What is the average number of trucks in the queue? truck(s) C. What is the average number of trucks in the system? truck(s) d. What is the average time a truck spends in the queue waiting for service? hour(s) e. What is the average time a truck spends in the system? hour(s) f. What is the probability that an arriving truck will have to wait? g. What is the probability that more than two trucks are waiting for service