Buff Tech, Inc. sells computer components and plans to borrow some money to expand. The company has a 12/31 year-end. After reading about earnings management (refer back to Chapter 4), Bucky, the owner has decided he should try to accelerate some sales to improve his financial statement ratios. He has called his best customers and asked them to make their usual January purchases and take delivery of the goods by December 31. He told the customers he would allow them until the end of February to pay for the purchases, just as if they had made the purchases in January.

Note: For revenue recognition purposes, the performance obligation was satisfied by 12/31.

Question:

What are the ethical implications of this plan? What ratios will be improved by accelerating these sales? What about future implications?

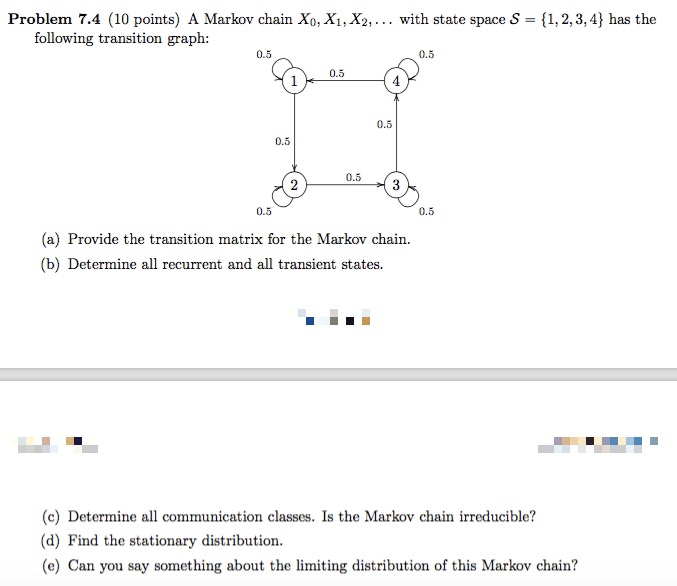
Which of the following is an advantage of multivariate correlational research over bivariate correlational research? O Bivariate correlational studies help address internal validity, whereas multivariate correlational studies do not. Multivariate correlational studies establish covariance, whereas bivariate correlational studies do not. O Some multivariate correlational studies help to address temporal precedence, whereas bivariate correlational studies do not. Multivariate correlational studies help to address external validity, whereas bivariate correlational studies do not.Problem 7.4 (10 points) A Markov chain Xo, X1, X2, ... with state space S = {1, 2,3, 4) has the following transition graph: 0.5 0.5 0.5 1 0.5 0.5 0.5 2 0.5 0.5 (a) Provide the transition matrix for the Markov chain. (b) Determine all recurrent and all transient states. (c) Determine all communication classes. Is the Markov chain irreducible? (d) Find the stationary distribution. (e) Can you say something about the limiting distribution of this Markov chain?1. Consider the Markov chain with the following transition matrix. 0 0.5 0.5 0.5 0 0.5 0.5 0.5 0 (a) Draw the transition diagram of the Markov chain. (b) Is the Markov chain ergodic? Give a reason for your answer. (c) Compute the two step transition matrix of the Markov chain. (d) What is the state distribution *2 for t = 2 if the initial state distribution for t = 0 is no = (0.1, 0.5, 0.4)