Question: Calculus 2 : Section 7.3: Problem 1 (1 point) Find the volume of the solid obtained by rotating the region bounded by y = 4
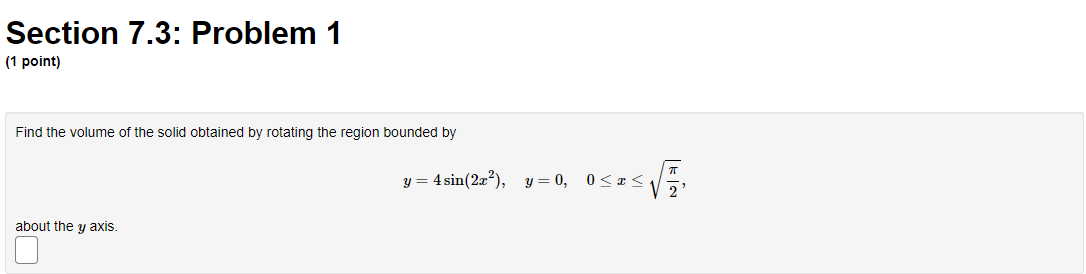

![= 4 sin(222), about the y axis. C] 24:0, Section 7.3: Problem](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6676870e6479b_8546676870e4e90b.jpg)
![volume generated by rotating the region bounded by y = e ],](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6676870ef1267_8546676870ee0e83.jpg)
Calculus 2 :

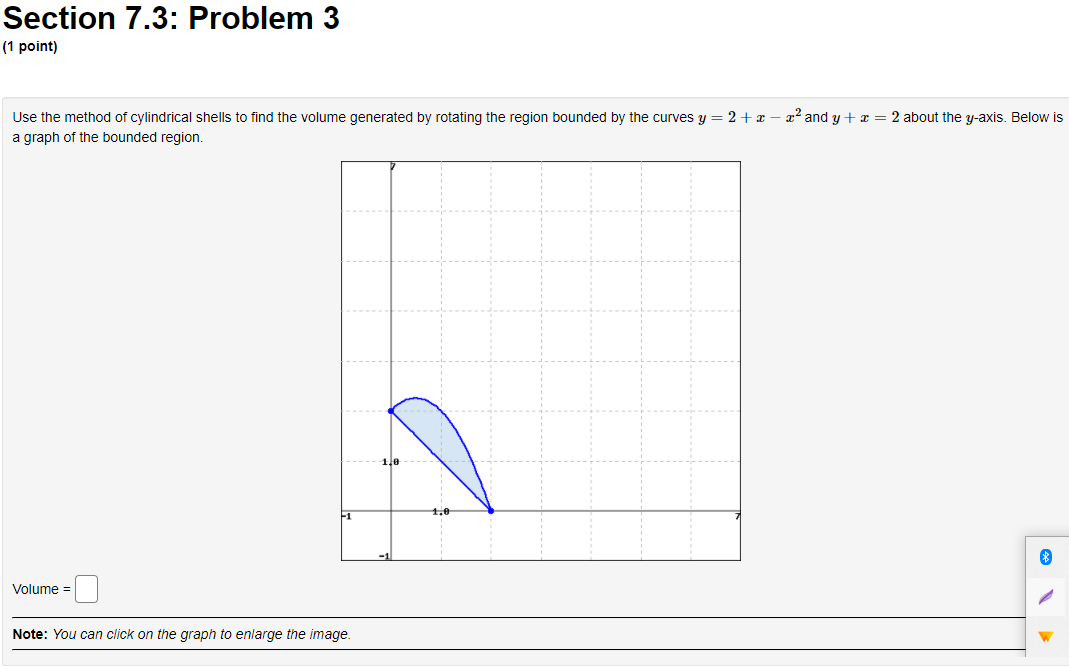

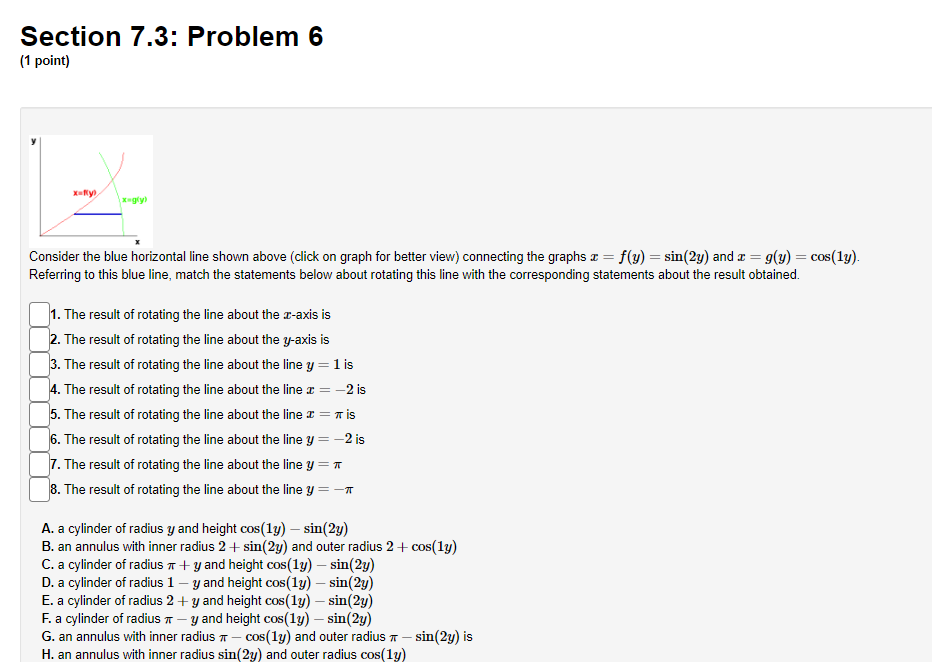
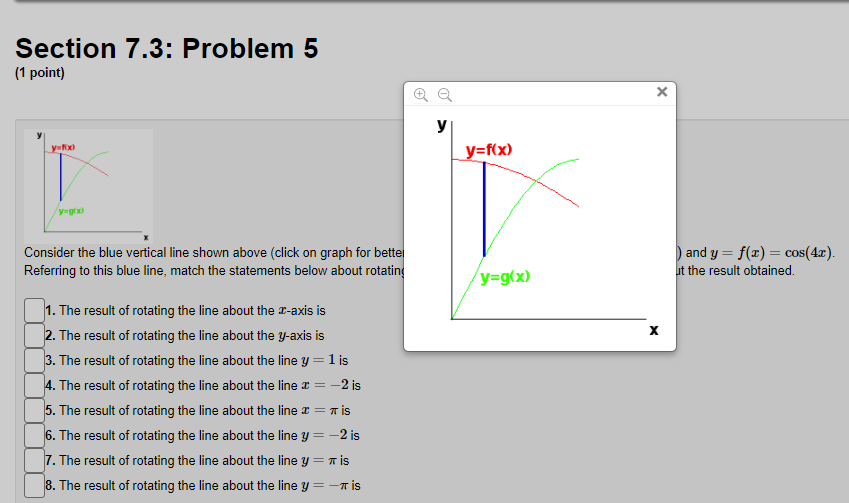
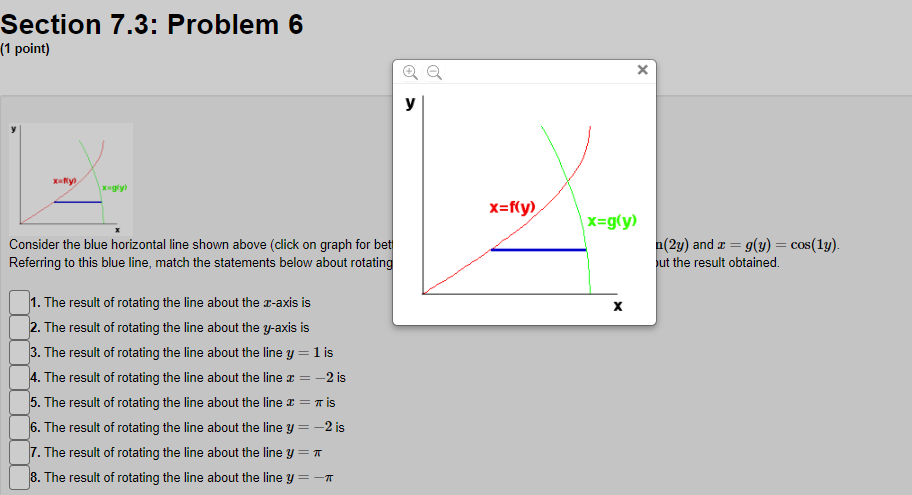
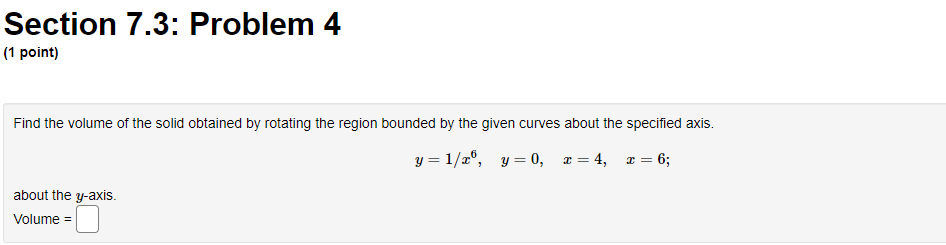
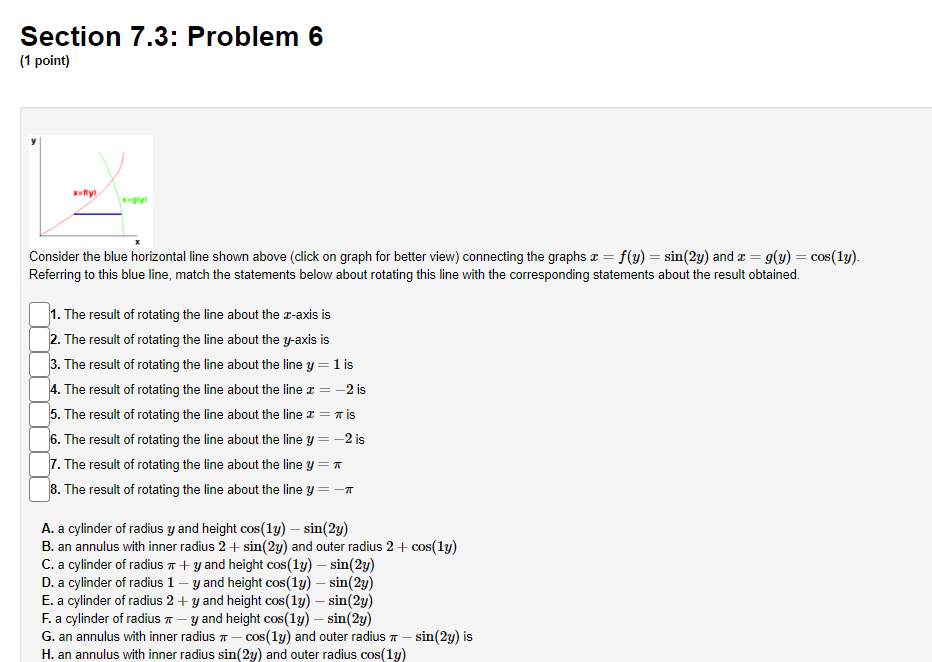
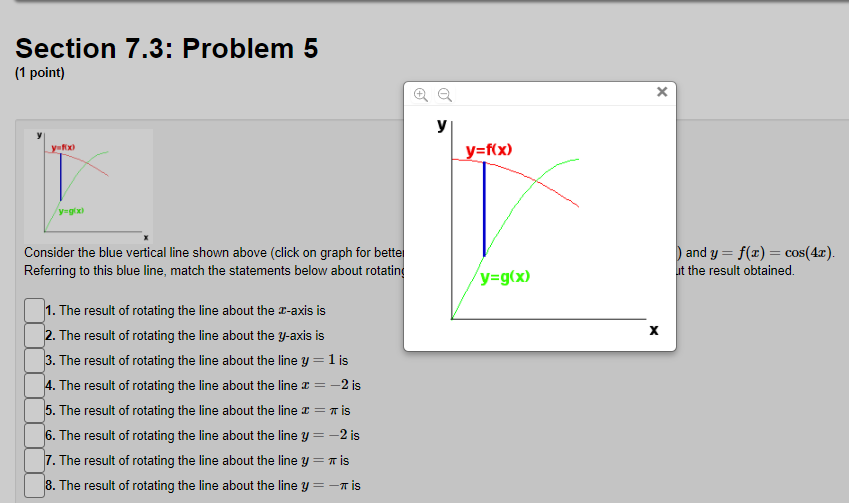
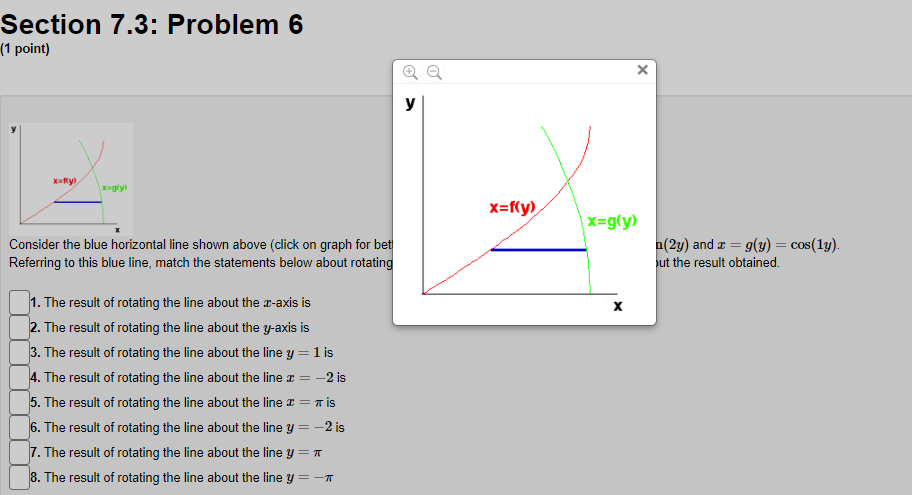
Section 7.3: Problem 1 (1 point) Find the volume of the solid obtained by rotating the region bounded by y = 4 sin(222), about the y axis. C] 24:0, Section 7.3: Problem 2 (1 point) Use the method of cylindrical shells to find the volume generated by rotating the region bounded by y = e ], y = 0, x = 0, and a = 1 about the y-axis. Volume =Section 7.3: Problem 3 (1 point) Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the curves y = 2 + x - x and y + x = 2 about the y-axis. Below is a graph of the bounded region. - 1/0 1.6 Volume = Note: You can click on the graph to enlarge the image.Section 7.3: Problem 4 (1 point) Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. y= 1/x', y=0, x=4, x=6; about the y-axis. Volume =Section 7.3: Problem 5 (1 point) y=Rx) y=g x) Consider the blue vertical line shown above (click on graph for better view) connecting the graphs y = g(x) = sin(x) and y = f(x) = cos(4x). Referring to this blue line, match the statements below about rotating this line with the corresponding statements about the result obtained. 1. The result of rotating the line about the I-axis is 2. The result of rotating the line about the y-axis is 3. The result of rotating the line about the line y = 1 is 4. The result of rotating the line about the line I = -2 is 5. The result of rotating the line about the line I = 7 is 6. The result of rotating the line about the line y = -2 is 7. The result of rotating the line about the line y = 7 is 8. The result of rotating the line about the line y = -7 is A. a cylinder of radius c and height cos(4x) - sin(I) B. an annulus with inner radius * + sin() and outer radius * + cos(4x) C. an annulus with inner radius 7 - cos(4x) and outer radius 7 - sin (I) D. an annulus with inner radius 1 - cos(4x) and outer radius 1 - sin(I) E. a cylinder of radius a + 2 and height cos(4x) - sin() F. an annulus with inner radius 2 + sin() and outer radius 2 + cos(4x) G. an annulus with inner radius sin () and outer radius cos(4x) H. a cylinder of radius 7 - I and height cos(4x) - sin(I)Section 7.3: Problem 6 {1 point] um I Consider the blue horizontal line shown above [click on graph for better View} connecting the graphs :5 2 y} 2 sin(2y} and z 2 y} 2 cosy). Referring to this blue line, match the statements below about rotating this line with the corresponding statements about the result obtained. 1. The result of rotating the line about the zaxis is . The result of rotating The line about the yards is 3. The result of rotating the line about the line 3; = 1 is .The result ofrotating the line about the line 3 = 2 is 5. The result of rotating the line about the line 3 = it is . The result of rotating the line about the line 3,! = 2 is . The result of rotating the line about the line 3; = 1r 8. The result of rotating the line about the line 3; = 1r A. a cylinder of radius 3; and height msy) sint2y) B. an annulus with inner radius 2 i sin[2y) and outer radius 2 i oos(1y} C. a cylinder of radius 11r+ y and height oos[1y) sin[2y) I}. a cylinder of radius 1 y and height moy) sin[2y) E. a cylinder ofradius 2 + y and height cos[ly) sin(2y} F. a cylinder of radius 1r y and height cos[1y) sin(2y) G. an annulus with inner radius :r oosy} and outer radius :1- siny] is H. an annulus with inner radius siny) and outer radius oos{1y) Section 7.3: Problem 5 (1 point) X KC y=f(x) y=g x) Consider the blue vertical line shown above (click on graph for better ) and y = f(x) = cos(4x). Referring to this blue line, match the statements below about rotating y=g(x) It the result obtained. 1. The result of rotating the line about the I-axis is 2. The result of rotating the line about the y-axis is X 3. The result of rotating the line about the line y = 1 is 4. The result of rotating the line about the line I = -2 is 5. The result of rotating the line about the line I = # is 6. The result of rotating the line about the line y = -2 is 7. The result of rotating the line about the line y = * is 8. The result of rotating the line about the line y = -7 isSection 7.3: Problem 6 (1 point) X y x=f(y) x=g(y) Consider the blue horizontal line shown above (click on graph for bet (2y) and x = g(y) = cos(ly). Referring to this blue line, match the statements below about rotating but the result obtained. 1. The result of rotating the line about the r-axis is X 2. The result of rotating the line about the y-axis is 3. The result of rotating the line about the line y = 1 is 4. The result of rotating the line about the line r = -2 is 5. The result of rotating the line about the line I = # is 6. The result of rotating the line about the line y = -2 is 7. The result of rotating the line about the line y = * 8. The result of rotating the line about the line y =
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


