Calculus 2:

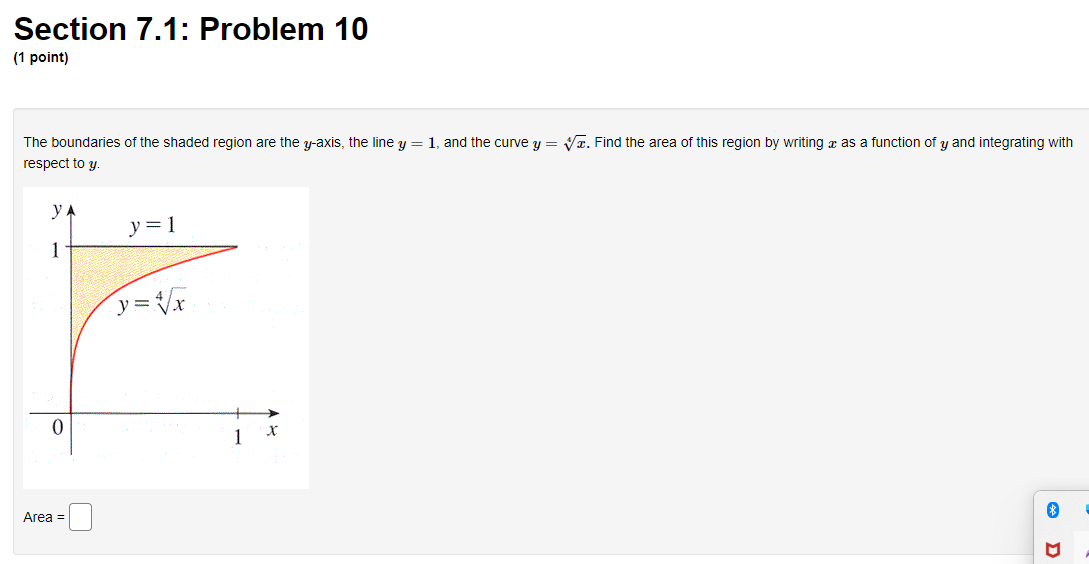
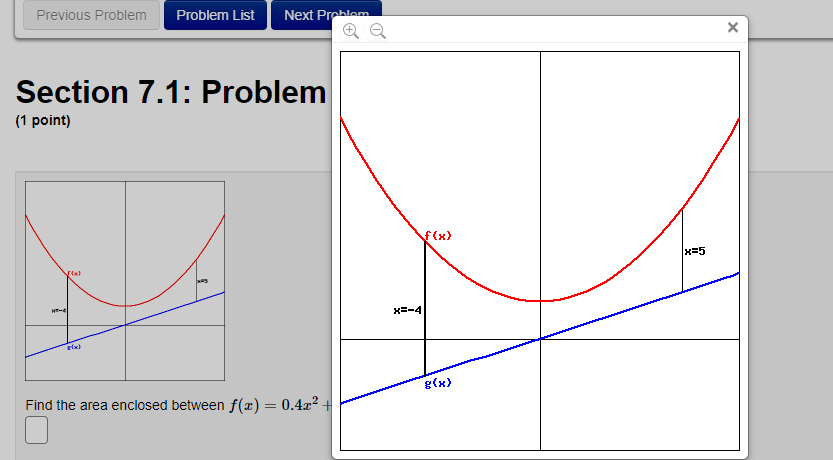
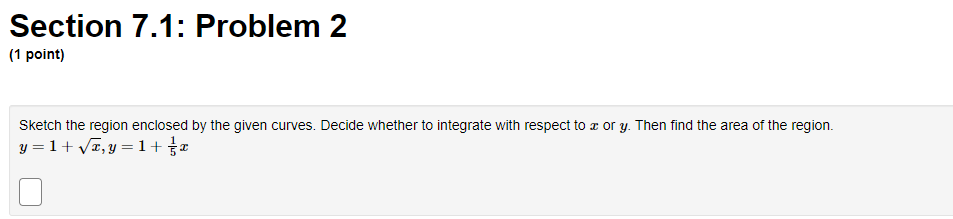
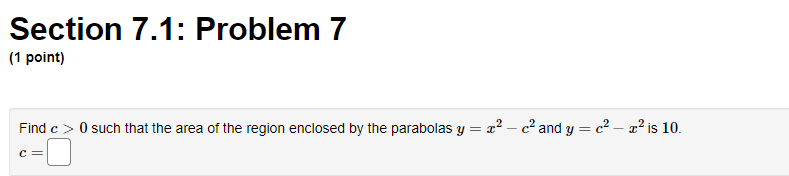
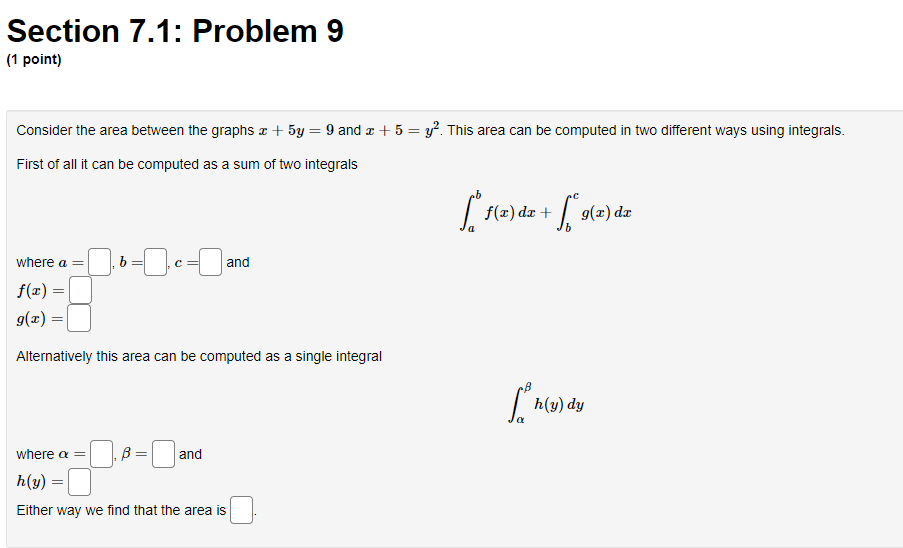
Section 7.1: Problem 1 (1 point: Find the area enclosed between x) 2 [1.422 + 4 and 9(3) 2 z from 2 = 4 to a: = 5. D Section 7.1: Problem 10 (1 point) The boundaiies of the shaded region are the yaxis, the line 3,! = Land the curve 5; = (/5. Find the area ottnis region by writing 2 as a function of y and integrating with respect to y. Previous Problem Problem List Next Problem X Section 7.1: Problem (1 point) f (x) X=5 *=-4 B(x) Find the area enclosed between f(x) = 0.4x2 +Section 7.1: Problem 2 [1 point) Sketch the region enclosed by the given curves. Decide whether to integrate with respect to z or 3:. Then nd the area of the region. y=1+E,y=1+%z C] Section 7.1: Problem 3 (1 point) Sketch the region enclosed by x = 4y and a + y = 3. Decide whether to integrate with respect to x or y. Then find the area of the region.Section 7.1: Problem 4 [1 point) Sketch the region enclosed by z + y2 = 30 and z = 3;. Decide whether to integrate with respect to m or 3:. Then nd the area of the region. B Section 7.1: Problem 5 (1 point) Sketch the region in the first quadrant enclosed by y = 9/x, y = 4x, and y = _ x. Decide whether to integrate with respect to x or y. Then find the area of the region. Area =Section 7.1: Problem 6 (1 point) Find the area of the region enclosed between y = 3 sin(x) and y = 2 cos(x) from = = 0 to x = 0.3x. Hint: Notice that this region consists of two parts.Section 7.1: Problem 7 (1 point) Find c > 0 such that the area of the region enclosed by the parabolas y = x - c' and y = c - x2 is 10. CSection 7.1: Problem 8 [1 point: Find the area of the region bounded by the parabola y = 552, the tangent line to this parabola at (2, 2D) and the z axis. C] Section 7.1: Problem 9 (1 point} Consider the area between the graphs 3 l 51:; = 9 and s l 5 = y2 This area can be computed in two different ways using integrals. First of all it can be computed as a sum of two integrals II c f z] dz +f 9(2) dz a E! where a. = ,b =D, .2 =D and fie} = 9(3) = Alternatively this area can be computed as a single integral 3 f My) y I} wherea =B,=C]and he) =E] Either wag,r we nd that the area is C]