Calculus 2 :

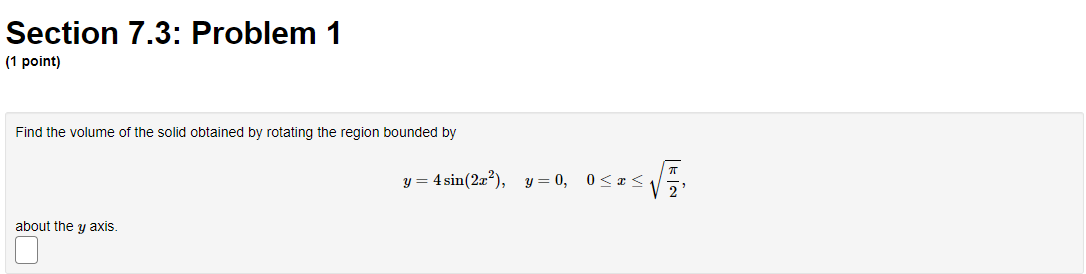
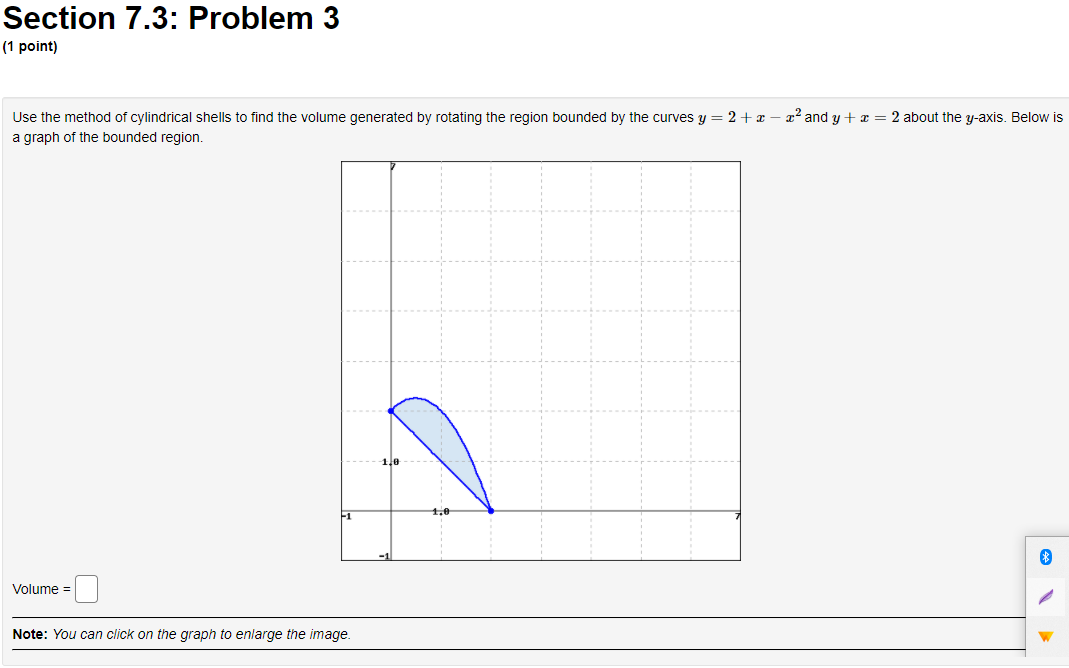
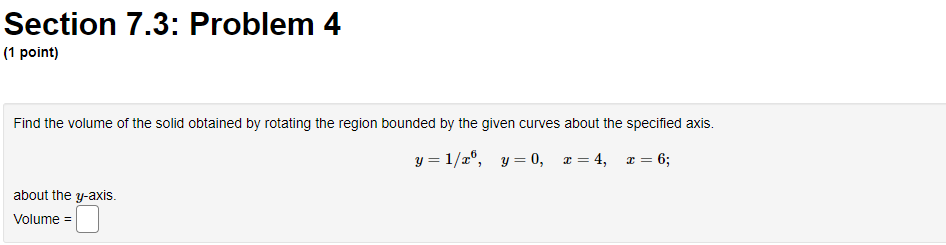
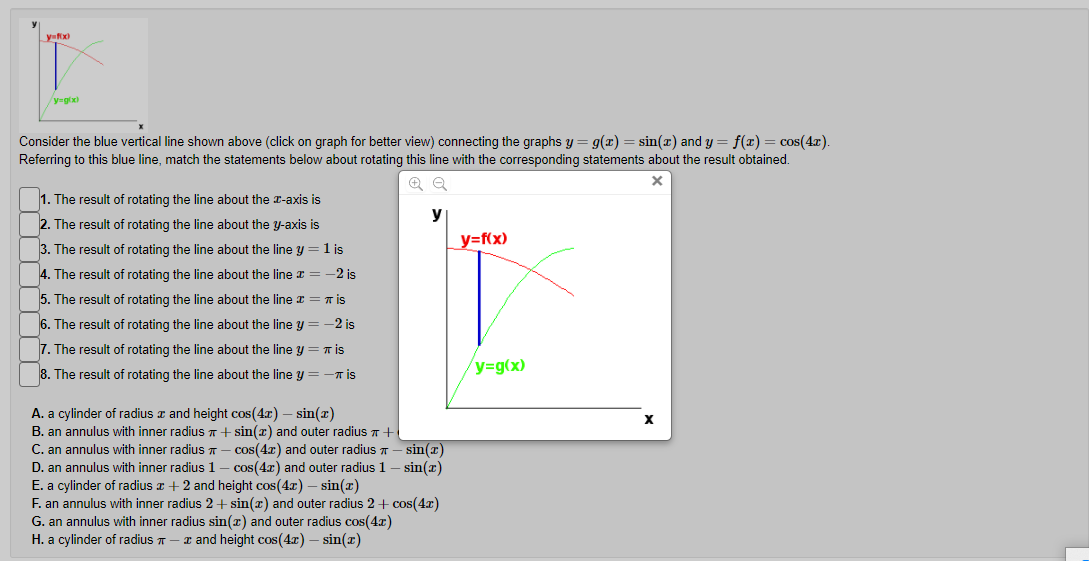
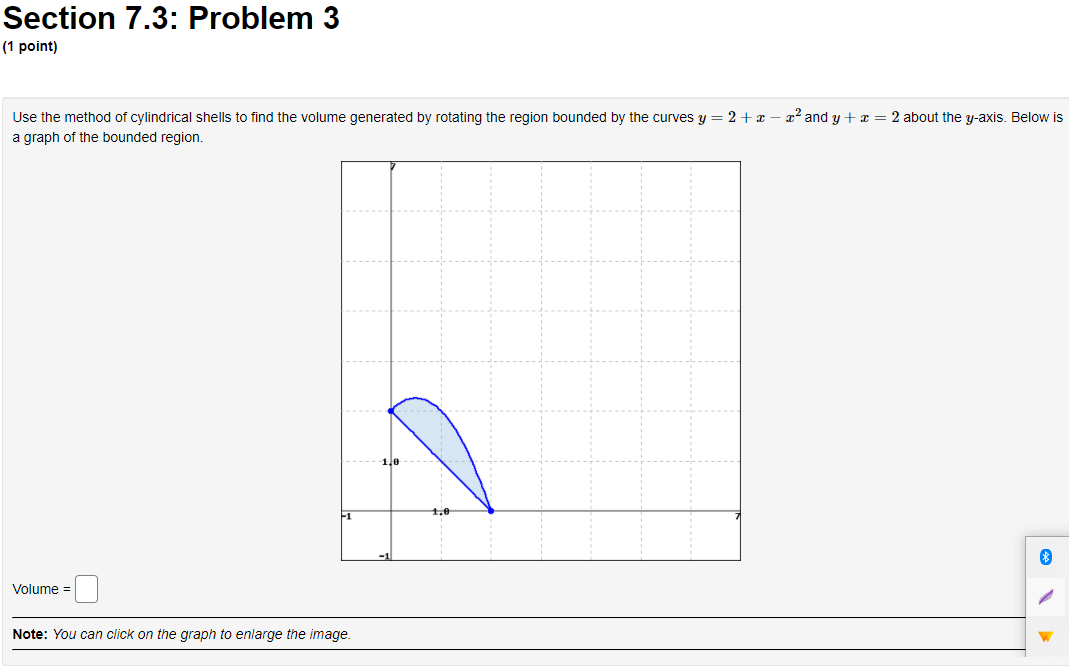
Section 7.3: Problem 1 (1 point) Find the volume of the solid obtained by rotating the region bounded by y = 4 sin(222), about the y axis. C] 24:0, Section 7.3: Problem 2 (1 point) Use the method of cylindrical shells to find the volume generated by rotating the region bounded by y = e ], y = 0, x = 0, and a = 1 about the y-axis. Volume =Section 7.3: Problem 3 (1 point) Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the curves y = 2 + x - x and y + x = 2 about the y-axis. Below is a graph of the bounded region. - 1/0 1.6 Volume = Note: You can click on the graph to enlarge the image.Section 7.3: Problem 4 (1 point) Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. y= 1/x', y=0, x=4, x=6; about the y-axis. Volume =Section 7.3: Problem 5 (1 point) y=Rx) y=g x) Consider the blue vertical line shown above (click on graph for better view) connecting the graphs y = g(x) = sin(x) and y = f(x) = cos(4x). Referring to this blue line, match the statements below about rotating this line with the corresponding statements about the result obtained. 1. The result of rotating the line about the I-axis is 2. The result of rotating the line about the y-axis is 3. The result of rotating the line about the line y = 1 is 4. The result of rotating the line about the line I = -2 is 5. The result of rotating the line about the line I = 7 is 6. The result of rotating the line about the line y = -2 is 7. The result of rotating the line about the line y = 7 is 8. The result of rotating the line about the line y = -7 is A. a cylinder of radius c and height cos(4x) - sin(I) B. an annulus with inner radius * + sin() and outer radius * + cos(4x) C. an annulus with inner radius 7 - cos(4x) and outer radius 7 - sin (I) D. an annulus with inner radius 1 - cos(4x) and outer radius 1 - sin(I) E. a cylinder of radius a + 2 and height cos(4x) - sin() F. an annulus with inner radius 2 + sin() and outer radius 2 + cos(4x) G. an annulus with inner radius sin () and outer radius cos(4x) H. a cylinder of radius 7 - I and height cos(4x) - sin(I)y=glx) Consider the blue vertical line shown above (click on graph for better view) connecting the graphs y = g(x) = sin(x) and y = f(x) = cos(4). Referring to this blue line, match the statements below about rotating this line with the corresponding statements about the result obtained. X 1. The result of rotating the line about the I-axis is 2. The result of rotating the line about the y-axis is y=f(x) 3. The result of rotating the line about the line y = 1 is 4. The result of rotating the line about the line I = -2 is 5. The result of rotating the line about the line I = # is 6. The result of rotating the line about the line y = -2 is 7. The result of rotating the line about the line y = * is 8. The result of rotating the line about the line y = - is y=g(x) A. a cylinder of radius x and height cos(4x) - sin(I) X B. an annulus with inner radius + + sin(x) and outer radius * + C. an annulus with inner radius * - cos(4x) and outer radius 7 - sin (I) D. an annulus with inner radius 1 - cos(4x) and outer radius 1 - sin(I) E. a cylinder of radius x + 2 and height cos(4x) - sin(I) F. an annulus with inner radius 2 + sin(x) and outer radius 2 + cos(4x) G. an annulus with inner radius sin() and outer radius cos(4x) H. a cylinder of radius 7 - I and height cos(4r) - sin(I)