Can u make a transfer function for a proportional controller for Heat Exchanger for Pasteurization of Milk or can u continue this equation? This section provides the mathematical model used in this process. This model is based on assumptions mentioned above.

The differential equations that govern the system were constructed using the framework outlined in Figure 3. By applying an energy balance to the incremental control volumes surrounding the hot fluid, the cold fluid, and the wall, the following differential equations were derived after simplification:

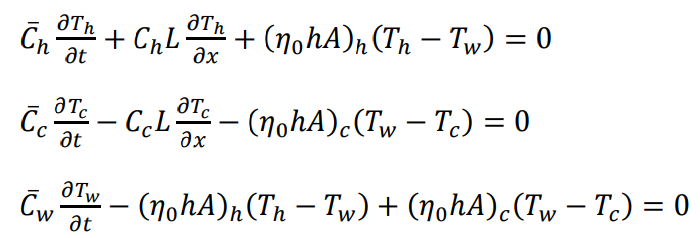
By disregarding the heat capacities of the heat exchanger walls (assume to be zero).

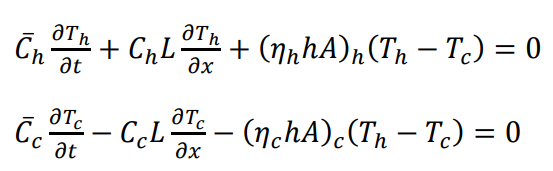
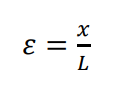New variable is defined,

Applying, the space (length) variable will always have a value between 0 and 1. We get:

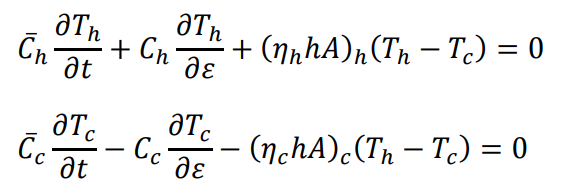
Indicating initial conditions,

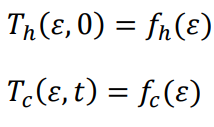
The temperature distribution has reached a steady state, the resulting temperature distribution can serve as the initial condition for subsequent calculations.

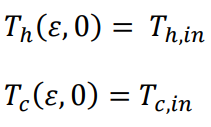
Boundary conditions:

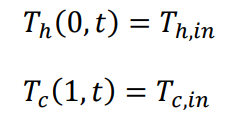
Applying heat balance on the outlet of each stream (at = 0 for hot stream and = 1 for cold stream),

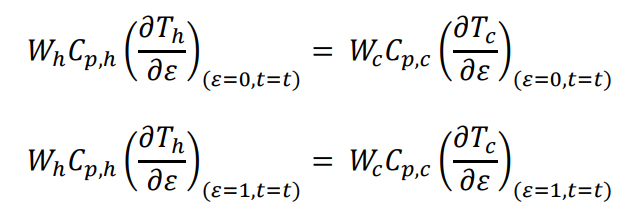
ChtTh+ChLxTh+(0hA)h(ThTw)=0CctTcCcLxTc(0hA)c(TwTc)=0CwtTw(0hA)h(ThTw)+(0hA)c(TwTc)=0 ChtTh+ChLxTh+(hhA)h(ThTc)=0CctTcCcLxTc(chA)c(ThTc)=0 =Lx ChtTh+ChTh+(hhA)h(ThTc)=0CctTcCcTc(chA)c(ThTc)=0 Th(,0)=fh()Tc(,t)=fc() Th(,0)=Th,inTc(,0)=Tc,in Th(0,t)=Th,inTc(1,t)=Tc,in WhCp,h(Th)(=0,t=t)=WcCp,c(Tc)(=0,t=t)WhCp,h(Th)(=1,t=t)=WcCp,c(Tc)(=1,t=t)