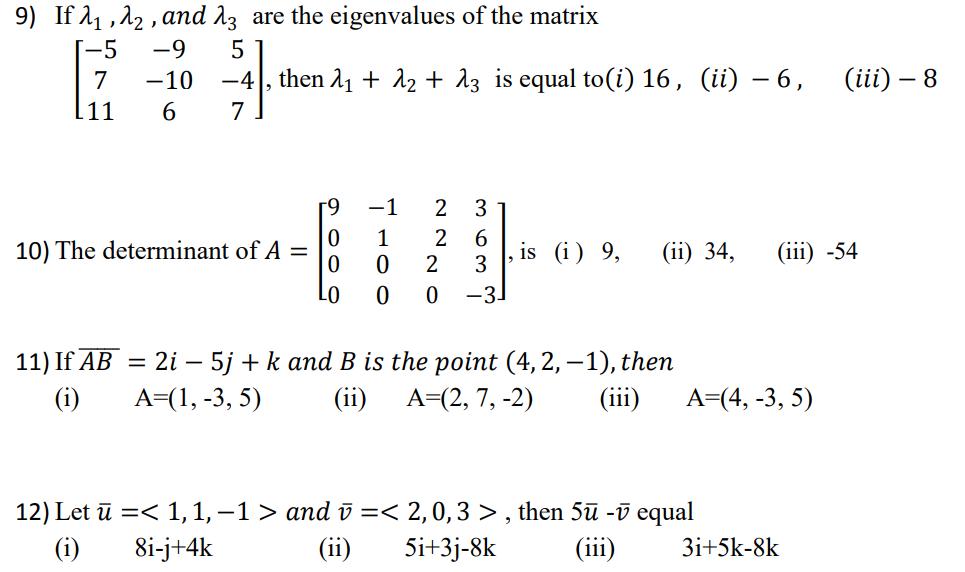Choose the correct answer and justify your answer: 1) If AB = 0 and BA # 0 then necessarily (i) A = 0 (ii) B= 0 (ii) %3D 0, - 0 (iv) #0, 20 2) If f(x) = x? + 3x + 4, then f (A) = A? + 3A + 41 (i) (ii)A? + 3A + 4 (iii)A? + 3A (iv) (A+ 4)(A+ I) 3) The vectors 2i + 3j - 4k and ai + bj + ck are perpendicular when i) %3D 4, b%3 2, %3D 4, ii) 3 4, b %3 4, %3D 5, iv) none of these. 4) The scalar projection of a vector A= i 2j + k on the vector B = 4i 4j+ 7k is 9 i1) 2; , ii) 10 iii) 19 5) The volume of a parallelepiped whose coterminous edges are represented by = 2i 3j +k, B =i-j+2k, =2i + j- k is i) 6, ii) 8, iii) 14 6) If the vectors 2i -j +k, i + 2j 3k and 3i + aj + 5k are coplanar, then i) a = 7, ii) a = 4, iii) a = -4 -2 1 7) The matrix A=| is given. The eigenvalues of 3A-1- 2A3 + 21 are (i) 16.9 , 56 (ii) 9, 12 (iii) 16.5, -51 8) The vectors =i-2k,B =j+ 3k are adjacent sides of parallelogram. Its area i) V14 , ii) V41 , ii) V7 9) If 11 ,22 , and 13 are the eigenvalues of the matrix -5 -9 5 then A1 + 12 + 13 is equal to(i) 16, (ii) 6, 7. 7 -10 -4 (iii) 8 11 6- -1 3 1 2 6. 10) The determinant of A = , is (i) 9, 3 (ii) 34, (iii) -54 2 -3- 01 11) If AB = 2i - 5j + k and B is the point (4, 2, 1), then (ii) (i) A=(1, -3, 5) A=(2, 7, -2) (iii) A=(4, -3, 5) 12) Let = < 1, 1, 1 > and v = < 2,0,3 >, then 5 -v equal (ii) (i) 8i-j+4k Si+3j-8k (iii) 3i+5k-8k