Computations\ In Exercises 1 through 4, find

q(x)

and

r(x)

as described by the division algorithm so that

f(x)=g(x)q(x)+r(x)

\ with

r(x)=0

or of degree less than the degree of

g(x)

.\

f(x)=x^(6)+3x^(5)+4x^(2)-3x+2

and

g(x)=x^(2)+2x-3

in

Z_(7)[x]

.\

f(x)=x^(6)+3x^(5)+4x^(2)-3x+2

and

g(x)=3x^(2)+2x-3

in

Z_(7)[x]

.\

f(x)=x^(5)-2x^(4)+3x-5

and

g(x)=2x+1

in

Z_(11)[x]

.\ 4)

f(x)=x^(4)+5x^(3)-3x^(2)

and

g(x)=5x^(2)-x+2

in

Z_(11)[x]

.\ I only need number 4 !

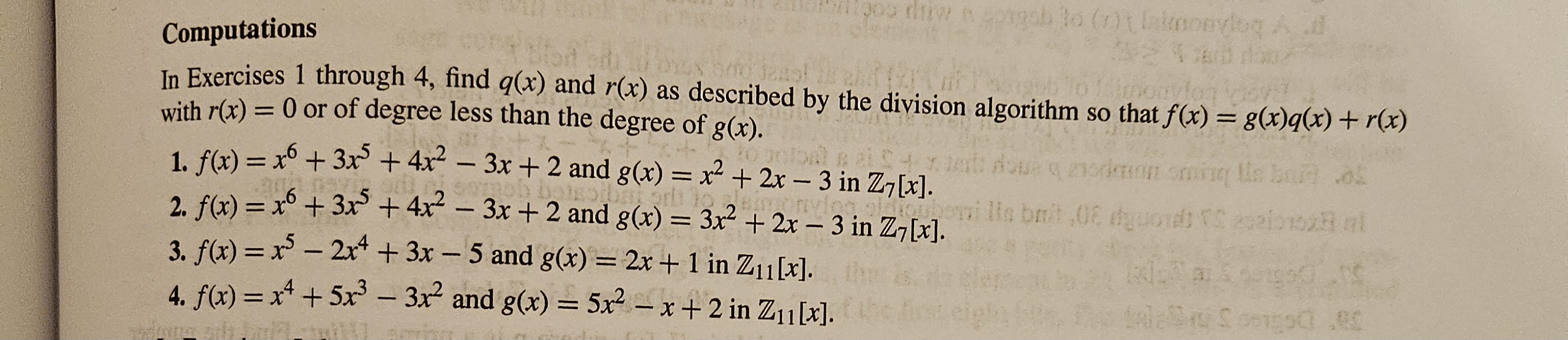
Computations In Exercises 1 through 4, find q(x) and r(x) as described by the division algorithm so that f(x)=g(x)q(x)+r(x) with r(x)=0 or of degree less than the degree of g(x). 1. f(x)=x6+3x5+4x23x+2 and g(x)=x2+2x3 in Z7[x] 2. f(x)=x6+3x5+4x23x+2 and g(x)=3x2+2x3 in Z7[x]. 3. f(x)=x52x4+3x5 and g(x)=2x+1 in Z11[x]. 4. f(x)=x4+5x33x2 and g(x)=5x2x+2 in Z11[x]