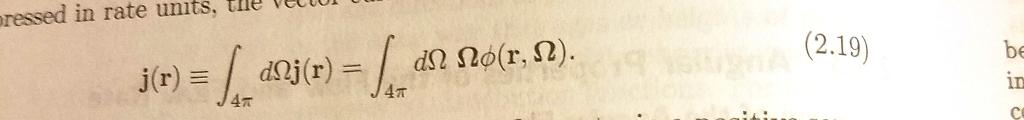
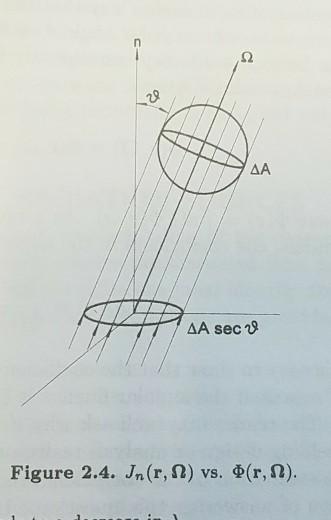
4. Consider a broad, uniform, unidirectional beam of particles intersecting a plane surface, as in Fig. 2.4. All particles travel in the direction = i sin , cos %. + j sin , sino + k cos do. The unit vector k is perpendicular to the plane and i, j, and k define an (x, y, z) Cartesian coordinate system. Show that the angular flux density (r, 2) can be written as o(r)8(w wo)8(-o), in which 8 represents the Dirac delta function and w cos. Use Eq. (2.19) to determine j(r), the current density. Show that the number of particles per unit time per unit area crossing the surface is woo(r), that is, that the z component of j is the number of particles per unit time crossing a unit area perpendicular to the z-axis. pressed in rate units, the dN No(r, N). j(r) = _dnj(r) = d Hi. (2.19) be in Ce AA sec Figure 2.4. Jn (r, 2) vs. (r, 2).