Consider a function shown below:\

f(t)={(0,0=3):}

\ (a) Obtain the Laplace transformation of the function given (HINT: when

L[f(t)]=F(s)

, the Laplace transform of the function with a time shift of

T

is given by\

{

(

:L[f(t-T)*1(t-T)]=F(s)e^(-sT))

}\ (b) Continue (a). Apply the Initial Value Theorem to

F(s)

and confirm

f(0)=0

.\ (c) Continue (a). Apply the Final Value Theorem to

F(s)

and confirm

f(\\\\infty )=1

. HINT: You may use L'Hospital's rule:

\\\\lim_(x->c)(f(x))/(g(x))=\\\\lim_(x->c)(f^(')(x))/(g^(')(x))

.

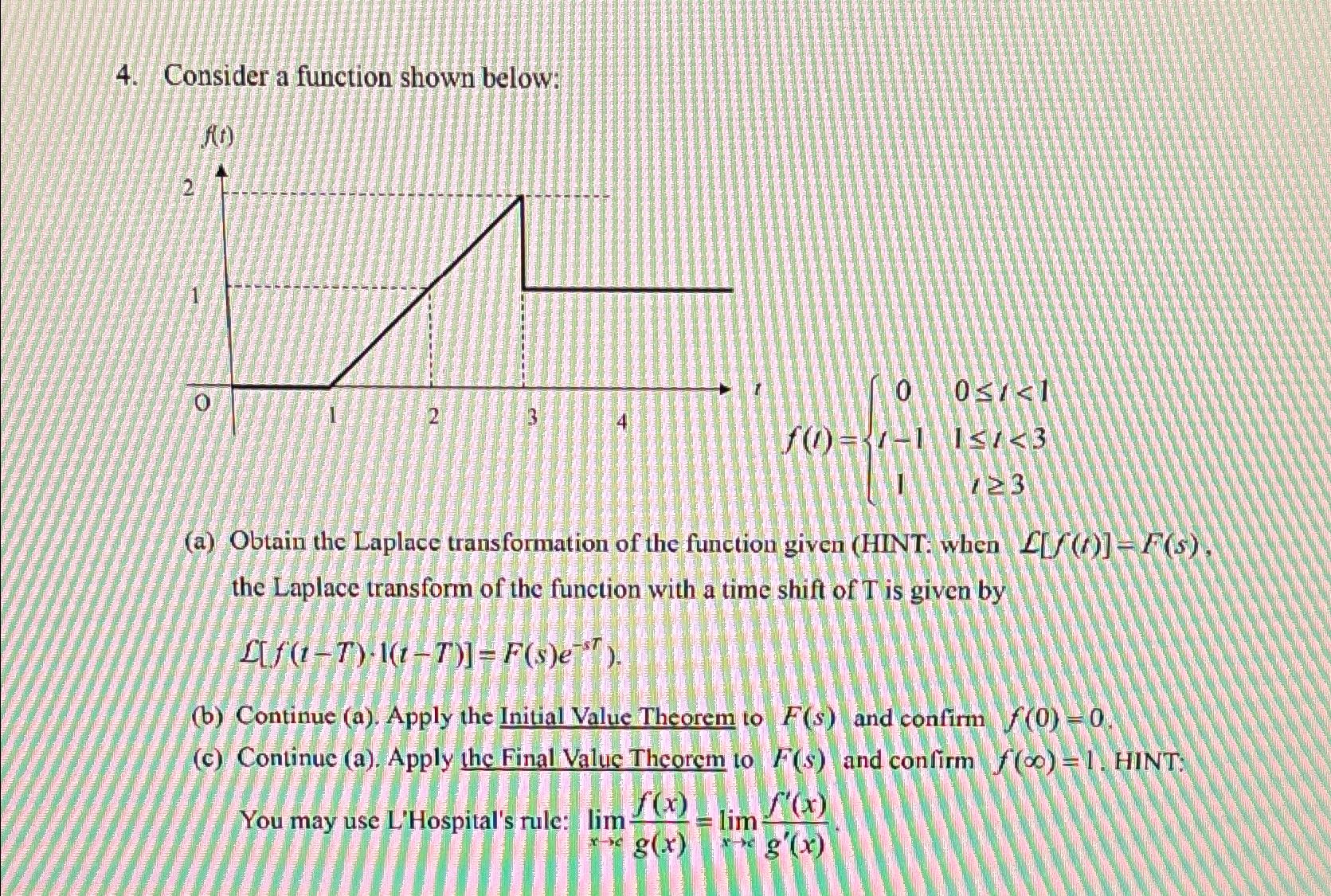
4. Consider a function shown below: f(t)=0t110t